Đề bài
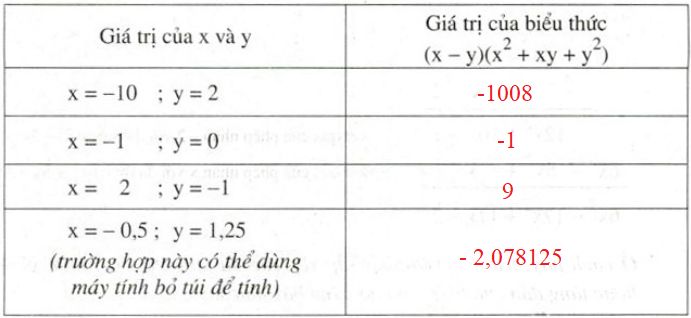
Điền kết quả tính được vào bảng:

Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Áp dụng qui tắc nhân đa thức với đa thức để nhân phá ngoặc rồi rút gọn biểu thức.
- Thay giá trị \(x, y\) tương ứng để tính giá trị của biểu thức.
Lời giải chi tiết
Trước hết, ta làm tính nhân để rút gọn biểu thức, ta được:
\(A={\left( {x - y} \right)\left( {{x^2} + xy + {y^2}} \right)}\)
\( = x\left( {{x^2} + xy + {y^2}} \right) - y\left( {{x^2} + xy + {y^2}} \right)\)
\( = x.{x^2} + x.xy + x.{y^2} + \left( { - y} \right).{x^2} \)\(+ \left( { - y} \right).xy + \left( { - y} \right).{y^2}\)
\( = {x^3} + {x^2}y + x{y^2}-y{x^2}-x{y^2}-{y^3} \)
\( = {x^3} + \left( {{x^2}y - y{x^2}} \right) + \left( {x{y^2} - x{y^2}} \right)\)\(\, - {y^3}\)
\(= {x^3}-{y^3}\)
Sau đó tính giá trị của biểu thức: \( A={x^3}-{y^3}\)
Ta có:
Khi \(x = -10; y = 2\) thì \(A = {\left( { - 10} \right)^3}-{2^3} = - 1000-8 \)\(= - 1008\)
Khi \(x = -1; y = 0\) thì \(A = {\left( { - 1} \right)^3}-{0^3} = - 1\)
Khi \(x = 2; y = -1\) thì \(A = {2^3}-{\left( { - 1} \right)^3} =8-(-1)= 8 + 1 = 9\)
Khi \(x = -0,5; y = 1,25\) thì
\(A = {\left( { - 0,5} \right)^3}-1,{25^3} \)\(= - 0,125-1,953125 = - 2,078125\)