Đề bài
Vẽ hai đường thẳng cắt nhau só cho trong các góc tạo thành có một cặp góc đối đỉnh có tổng số đo bằng 130o. Tính số đo mỗi góc có trên hình.
Phương pháp giải - Xem chi tiết
2 góc kề bù có tổng số đo là \(180^0\)
Lời giải chi tiết
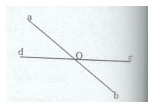
Theo đầu bài ta có: \(\widehat {aOd}\) và \(\widehat {bOc}\) đối đỉnh và \(\widehat {aOd} + \widehat {bOc} = {130^0}.\)
Ta có: \(\widehat {aOd} = \widehat {bOc}\) (hai góc đối đỉnh) nên \(2.\widehat {aOd} = {130^0} \Rightarrow \widehat {aOd} = {130^0}:2 = {65^0}\)
Do đó: \(\widehat {bOc} = \widehat {aOd} = {65^0}\)
Mà \(\widehat {aOd} + \widehat {aOc} = {180^0}\) (kề bù).
Nên \({65^0} + \widehat {aOc} = {180^0} \Rightarrow \widehat {aOc} = {180^0} - {65^0} = {115^0}.\)
\(\widehat {bOd} = \widehat {aOc}\) (hai góc đối đỉnh) nên \(\widehat {bOd} = {115^0}.\)
Ta còn có: \(\widehat {aOb} = {180^0},\widehat {cOd} = {180^0}.\)
soanvan.me
