Đề bài
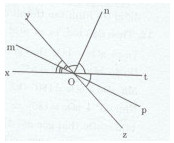
Cho hai góc kề bù \(\widehat {xOy}\)và \(\widehat {yOt}\) . Gouj Om, On lần lượt là tia phân giác của \(\widehat {xOy}\) và \(\widehat {yOt}\).
a) Tính số đo \(\widehat {mOn}\)
b) Vẽ \(\widehat {tOz}\) là góc đối đỉnh của \(\widehat {xOy}\), vẽ tia Op là tia đối của tia Om. Chứng tỏ rằng Op, On lần lượt là tia phân giác của \(\widehat {tOz}\) và \(\widehat {mOp}\)
Lời giải chi tiết
a)Ta có: \(\widehat {xOy}\) và \(\widehat {yOt}\) là hai góc kề bù.
Nên \(\widehat {xOy} + \widehat {yOt} = {180^0}\)
Mà \(\widehat {mOy} = {1 \over 2}\widehat {xOy}\) (Om là tia phân giác của góc xOy)
Và \(\widehat {yOn} = {1 \over 2}\widehat {yOt}\) (On là tia phân giác của góc yOt)
Do đó:
\(\eqalign{ & \widehat {mOn} = \widehat {mOy} + \widehat {yOn} \cr & = {1 \over 2}\widehat {xOy} + {1 \over 2}\widehat {yOt} = {1 \over 2}(\widehat {xOy} + \widehat {yOt}) = {1 \over 2}{.180^0} = {90^0} \cr} \)
b) Ta có: \(\widehat {xOm} = \widehat {mOy}\) (Om là tia phân giác của \(\widehat {xOy})\)
\(\widehat {xOm} = \widehat {tOp}\) (hai góc đối đỉnh)
\(\widehat {mOy} = \widehat {pOz}\) (hai góc đối đỉnh)
Do đó: \(\widehat {tOP} = \widehat {pOz}.\) Vậy Op là tia phân giác của góc tOz
Ta cũng có: \(\widehat {yOm} = \widehat {tOp}\)
Mà \(\widehat {yOn} = \widehat {nOt}\) (On là tia phân giác góc yOt). Do đó \(\widehat {yOm} + \widehat {yOn} = \widehat {tOp} + \widehat {nOt}\)
Suy ra \(\widehat {mOn} = \widehat {pOn}.\) Vậy On là tia phân giác của góc mOp.
soanvan.me
