Đề bài
Cho góc tù xOy. Trong góc xOy vẽ tia Om vuông góc với Ox và tia On vuông góc với tia Oy.
a) Chứng tỏ rằng \(\widehat {xOn} = \widehat {mOy}\)
b) Tính số đo góc \(\widehat {xOy} + \widehat {mOn}\)
c) Gọi Ot là tia phân giác của góc xOy. Chứng minh rằng Ot là tia phân giác của góc mOn.
Lời giải chi tiết
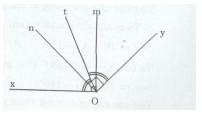
a)Ta có: \(Om \bot 0x \Rightarrow \widehat {m0x} = {90^0}\) và \(On \bot Oy \Rightarrow \widehat {nOy} = {90^0}\)
Do đó: \(\widehat {m0x} = \widehat {nOy}({90^0})(1)\)
Tia On nằm trong \(\widehat {xOy} \Rightarrow \widehat {xOn} + \widehat {nOy} = \widehat {xOy}\)
Và tia Om nằm trong \(\widehat {xOy} \Rightarrow \widehat {mOy} + \widehat {m0x} = \widehat {xOy}\)
Nên \(\widehat {xOn} + \widehat {nOy} = \widehat {mOy} + \widehat {m0x}(2)\)
Từ (1) và (2) ta có: \(\widehat {xOn} = \widehat {mOy}\)
b) Ta có: \(\eqalign{ & \widehat {xOy} + \widehat {mOn} = \widehat {nOy} + \widehat {xOn} + \widehat {mOn} \cr & = {90^0} + \widehat {mOy} + \widehat {mOn} = {90^0} + \widehat {nOy} = {90^0} + {90^0} = {180^0} \cr} \)
c) Ta có: Ot là tia phân giác góc \(\widehat {xOy} \Rightarrow \widehat {xOt} = \widehat {yOt} \Rightarrow \widehat {xOn} + \widehat {nOt} = \widehat {yOm} + \widehat {mOt}\)
Mà \(\widehat {xOn} = \widehat {mOy}\) (câu a) \( \Rightarrow \widehat {nOt} = \widehat {mOt}\)
Mà tia Ot nằm giữa hai tia Om và On => Ot là tia phân giác góc mOn.
soanvan.me
