Đề bài
Tìm x trong các hình vẽ sau:
Lời giải chi tiết
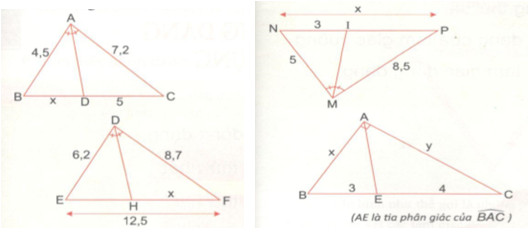
•∆ABC có AD là đường phân giác (gt)\( \Rightarrow {{DB} \over {DC}} = {{AB} \over {AC}}\)
Nên \({x \over 5} = {{4,5} \over {7,2}} \Rightarrow x = {{5.4,5} \over {7,2}} = 3,125\)
•∆DEF có DH là đường phân giác (gt)
\( \Rightarrow {{HE} \over {HF}} = {{DE} \over {DF}}\)
\(\Rightarrow {{HE} \over {DE}} = {{HF} \over {DF}} = {{HE + HF} \over {DE + DF}} = {{EF} \over {DE + DF}}\)
Ta có \({{HF} \over {DF}} = {{EF} \over {DE + DF}}\) nên \({x \over {8,7}} = {{12,5} \over {6,2 + 8,7}} \Rightarrow x = {{8,7.12,5} \over {6,2 + 8,7}} \approx 7,3\)
•∆MNP có MI là đường phân giác (gt)
\( \Rightarrow {{IN} \over {IP}} = {{MN} \over {MP}}\)
\(\Rightarrow {{IN} \over {MN}} = {{IP} \over {MP}} = {{IN + IP} \over {MN + MP}} = {{NP} \over {MN + MP}}\)
Ta có: \({{IN} \over {MN}} = {{NP} \over {MN + MP}}\) nên \({3 \over 5} = {x \over {5 + 8,5}} \Rightarrow x = {{3.(5 + 8,5)} \over {}}5 = 8,1\)
•BC = BE + EC = 3 + 4 = 7
∆ABC có AE là đường phân giác (gt) nên:
\({{EB} \over {EC}} = {{AB} \over {AC}} \)
\(\Rightarrow {3 \over 4} = {x \over y} \Rightarrow {y \over 4} = {x \over 3} \Rightarrow {{{y^2}} \over {16}} = {{{x^2}} \over 9}\)
Mặt khác ∆ABC vuông tại A có \(A{B^2} + A{C^2} = B{C^2}\) (Định lí Py-ta-go)
\( \Rightarrow {x^2} + {y^2} = {7^2} = 49\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có: \({{{y^2}} \over {16}} = {{{x^2}} \over 9} = {{{y^2} + {x^2}} \over {16 + 9}} = {{49} \over {25}}\)
Do đó \({x^2} = {{9.49} \over {25}} = 17,64 = 4,{2^2}\) . Mà x > 0 nên x = 4,2
soanvan.me
