Đề bài
Cho hình hộp ABCD.A’B’C’D’. Một đường thẳng ∆ cắt các đường thẳng AA’, BC, C’D’ lần lượt tại M, N, P sao cho \(\overrightarrow {NM} = 2\overrightarrow {NP} \) . Tính \({{MA} \over {MA'}}\)
Lời giải chi tiết
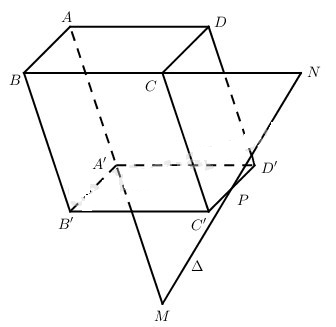
Đặt \(\overrightarrow {A{\rm{D}}} = \overrightarrow a ,\overrightarrow {AB} = \overrightarrow b ,\overrightarrow {AA'} = \overrightarrow c \) . Vì M thuộc đường thẳng AA’ nên
\(\overrightarrow {AM} = k\overrightarrow {AA'} = k\overrightarrow c \).
N là điểm thuộc đường thẳng BC nên \(\overrightarrow {BN} = l\overrightarrow a \);
P là điểm thuộc đường thẳng C’D’ nên \(\overrightarrow {C'P} = m\overrightarrow b \)
Với k, l, m là những số thực.
Ta có:
\(\eqalign{ & \overrightarrow {NM} = \overrightarrow {NB} + \overrightarrow {BA} + \overrightarrow {AM} = - l\overrightarrow a - \overrightarrow b + k\overrightarrow c \cr & \overrightarrow {NP} = \overrightarrow {NB} + \overrightarrow {BB'} + \overrightarrow {B'C'} + \overrightarrow {C'P'} \cr & = - l\overrightarrow a + \overrightarrow c + \overrightarrow a + m\overrightarrow b \cr & = \left( {1 - l} \right)\overrightarrow a + m\overrightarrow b + \overrightarrow c \cr} \)
Do \(\overrightarrow {NM} = 2\overrightarrow {NP} \) nên ta có:
\(\left\{ \matrix{ - l = 2\left( {1 - l} \right) \hfill \cr - 1 = 2m \hfill \cr k = 2 \hfill \cr} \right. \Rightarrow k = 2,m = - {1 \over 2},l = 2\)
Vậy \({{MA} \over {MA'}} = 2\)
soanvan.me
