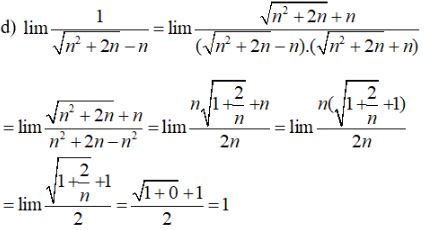Tính các giới hạn sau:
LG a
\(\lim \sqrt {3{n^4} - 10n + 12} \)
Lời giải chi tiết:
\(\lim \sqrt {3{n^4} - 10n + 12} \) \(= \lim {n^2}.\sqrt {3 - {{10} \over {{n^3}}} + {{12} \over {{n^4}}}} \) \(= + \infty \)
Vì
\(\left\{ \begin{array}{l}
\lim {n^2} = + \infty \\
\lim \sqrt {3 - \frac{{10}}{{{n^3}}} + \frac{{12}}{{{n^4}}}} = \sqrt 3 > 0
\end{array} \right.\)
LG b
\(\lim \left( {{{2.3}^n} - {{5.4}^n}} \right)\)
Lời giải chi tiết:
\(\lim \left( {{{2.3}^n} - {{5.4}^n}} \right) \) \(= \lim {4^n}\left[ {2{{\left( {{3 \over 4}} \right)}^n} - 5} \right] = - \infty \)
Vì
\(\left\{ \begin{array}{l}
\lim {4^n} = + \infty \\
\lim \left( {2.{{\left( {\frac{3}{4}} \right)}^n} - 5} \right) = - 5 < 0
\end{array} \right.\)
LG c
\(\lim \left( {\sqrt {{n^4} + {n^2} + 1} - {n^2}} \right)\)
Lời giải chi tiết:
\(\eqalign{ & \lim \left( {\sqrt {{n^4} + {n^2} + 1} - {n^2}} \right) \cr& = \lim \frac{{\left( {\sqrt {{n^4} + {n^2} + 1} - {n^2}} \right)\left( {\sqrt {{n^4} + {n^2} + 1} + {n^2}} \right)}}{{\sqrt {{n^4} + {n^2} + 1} + {n^2}}} \cr &= \lim \frac{{{n^4} + {n^2} + 1 - {n^4}}}{{\sqrt {{n^4} + {n^2} + 1} + {n^2}}}\cr &= \lim {{{n^2} + 1} \over {\sqrt {{n^4} + {n^2} + 1} + {n^2}}} \cr & = \lim \frac{{{n^2} + 1}}{{\sqrt {{n^4}\left( {1 + \frac{1}{{{n^2}}} + \frac{1}{{{n^4}}}} \right)} + {n^2}}} \cr & = \lim \frac{{{n^2}\left( {1 + \frac{1}{{{n^2}}}} \right)}}{{{n^2}\sqrt {1 + \frac{1}{{{n^2}}} + \frac{1}{{{n^4}}}} + {n^2}}} \cr & = \lim \frac{{{n^2}\left( {1 + \frac{1}{{{n^2}}}} \right)}}{{{n^2}\left( {\sqrt {1 + \frac{1}{{{n^2}}} + \frac{1}{{{n^4}}}} + 1} \right)}}\cr & = \lim {{1 + {1 \over {{n^2}}}} \over {\sqrt {1 + {1 \over {{n^2}}} + {1 \over {{n^4}}}} + 1}} \cr & = \frac{{1 + 0}}{{\sqrt {1 + 0 + 0} + 1}}= {1 \over 2} \cr} \)
LG d
\(\lim {1 \over {\sqrt {{n^2} + 2n} - n}}\)
Lời giải chi tiết:
soanvan.me