Đề bài
Giải phương trình
\(\tan x = \cot 2x\)
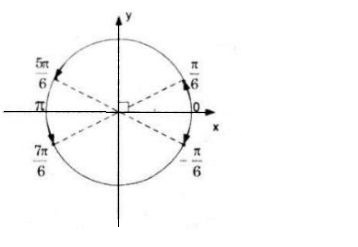
Biểu diễn các nghiệm trên đường tròn lượng giác.
Lời giải chi tiết
Điều kiện
\(\left\{ \begin{array}{l}
\cos x \ne 0\\
\sin 2x = 2\sin x\cos x \ne 0
\end{array} \right.\)
\( \Leftrightarrow \left\{ {\matrix{ {\sin x \ne 0} \cr {\cos x \ne 0} \cr } } \right. \Leftrightarrow x \ne k{\pi \over 2}\)
\(\eqalign{ & \tan x = \cot 2x \Leftrightarrow {{\sin x} \over {\cos x}} = {{\cos 2x} \over {\sin 2x}} \cr& \Rightarrow\cos x \cos 2x - \sin x\sin 2x = 0 \cr & \Leftrightarrow \cos 3x = 0 \cr & \Leftrightarrow 4{\cos ^3}x - 3\cos x = 0\cr &\Leftrightarrow \cos x\left( {4{{\cos }^2}x - 3} \right) = 0 \cr & \Leftrightarrow {\cos ^2}x = {3 \over 4} (do\, \cos x\ne 0) \cr & \Leftrightarrow {{1 + \cos 2x} \over 2} = {3 \over 4} \Leftrightarrow \cos 2x = {1 \over 2} \cr & \Leftrightarrow x =\pm {\pi \over 6} + k\pi (k\in\mathbb Z) \cr} \)
Biểu diễn nghiệm trên đường tròn được 4 điểm.
Cách khác:
soanvan.me
