Đề bài
Cho hình chóp A.ABCD có cạnh SA = x, tất cả các cạnh còn lại có độ dài bằng a.
a) Chứng minh rằng SAC là tam giác vuông.
b) Tính đường cao SH của hình chóp đã cho.
Lời giải chi tiết
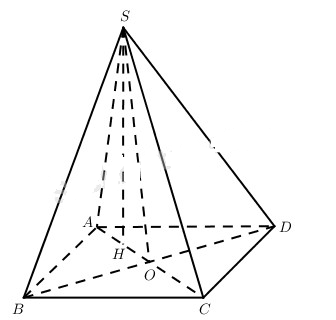
a) Gọi O là giao điểm của AC và BD thì \(OA = OC,OB = O{\rm{D}}\).
Vì \(SB = S{\rm{D}} = CB = C{\rm{D}}\) nên \(\Delta BC{\rm{D}} = \Delta B{\rm{SD}}\), từ đó \(SO = OC = OA\).
Vậy SAC là tam giác vuông tại S.
b) \(\left. \matrix{ AC \bot B{\rm{D}} \hfill \cr {\rm{SO}} \bot {\rm{BD}} \hfill \cr} \right\} \Rightarrow B{\rm{D}} \bot \left( {SAC} \right)\),
từ đó \(\left( {SAC} \right) \bot \left( {ABC{\rm{D}}} \right)\).
Vậy nếu kẻ đường cao SH của tam giác SAC thì \(SH \bot \left( {ABC{\rm{D}}} \right)\),
do đó \(d\left( {S;mp\left( {ABC{\rm{D}}} \right)} \right) = SH = {{SA.SC} \over {AC}} = {{a.x} \over {\sqrt {{a^2} + {x^2}} }}\).
soanvan.me
