Đề bài
Đáy của hình chóp A.BCD là tam giác đều. Đường cao của hình chóp kẻ từ đỉnh A đi qua trung điểm H của cạnh CD. Cắt hình chóp đó bởi mặt phẳng song song với AB và CD và cách đỉnh B một khoảng bằng d. Tính diện tích thiết diện thu được, biết cạnh của tam giác đều BCD là a và \(AB = a\sqrt 2 \).
Lời giải chi tiết
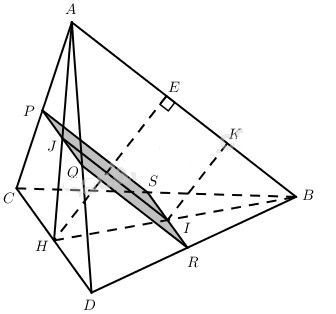
Dễ thấy thiết diện là hình bình hành PQRS. Mặt khác theo giả thiết \(C{\rm{D}} \bot \left( {AHB} \right)\) nên \(C{\rm{D}} \bot AB\). Vậy PQRS là hình chữ nhật.
Kẻ \(HE \bot AB\) thì \(HE \bot \left( {PQ{\rm{RS}}} \right)\). Kẻ IK // HE thì \(IK \bot \left( {PQ{\rm{RS}}} \right)\). Do AB // (PQRS) và \(d\left( {B;\left( {PQ{\rm{RS}}} \right)} \right) = d\) nên IK = d.
Ta có
\(HE = {{AH.HB} \over {AB}} = {{\sqrt {A{B^2} - B{H^2}} .HB} \over {AB}} = {{a\sqrt {15} } \over {4\sqrt 2 }}\)
Lại có
\(\eqalign{ & {{IK} \over {HE}} = {{BI} \over {BH}} = {{R{\rm{S}}} \over {C{\rm{D}}}} \cr & \Rightarrow R{\rm{S}} = {{da} \over {a\sqrt {15} }}.4\sqrt 2 = {{4\sqrt 2 d} \over {\sqrt {15} }}; \cr & BI = {{IK.BH} \over {HE}} = {{d.{{a\sqrt 3 } \over 2}} \over {{{a\sqrt {15} } \over {4\sqrt 2 }}}} = {{2\sqrt 2 d} \over {\sqrt 5 }} \cr} \)
Mặt khác \({{IJ} \over {AB}} = {{HI} \over {HB}} = {{\left( {HB - IB} \right)} \over {HB}};\)
Từ đó \(IJ = {{AB\left( {HB - IB} \right)} \over {HB}} = {{\sqrt 2 \left( {a\sqrt {15} - 4\sqrt 2 d} \right)} \over {\sqrt {15} }}\)
Vậy \({S_{PQ{\rm{RS}}}} = R{\rm{S}}.IJ = {8 \over {15}}d\left( {a\sqrt {15} - 4\sqrt 2 d} \right)\) .
soanvan.me
