Đề bài
Thực hành 1 trang 14
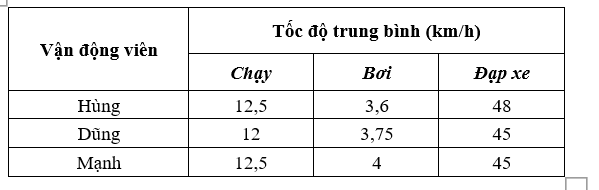
Ba vận động viên Hùng, Dũng và Mạnh tham gia thi đấu nội dung ba môn phối hợp: chạy, bơi và đạp xe, trong đó tốc độ trung bình của họ trên mỗi chặng đua được cho ở bảng dưới đây.
Biết tổng thời gian thi đấu ba môn phối hợp của Hùng là 1 giờ 1 phút 30 giây, của Dũng là 1 giờ 3 phút 40 giây và của Mạnh là 1 giờ 1 phút 55 giây. Tính cự li của mỗi chặng đua.
Lời giải chi tiết
Gọi cự li của mỗi chặng đua chạy, bơi và đạp xe là x,y,z (đơn vị km) (\(x,y,z > 0\))
Tổng thời gian thi đấu ba môn phối hợp của Hùng là 1 giờ 1 phút 30 giây = 1,025 giờ, nên ta có:
\(\frac{x}{{12,5}} + \frac{y}{{3,6}} + \frac{z}{{48}} = 1,025\)
Tổng thời gian thi đấu ba môn phối hợp của Dũng là 1 giờ 3 phút 40 giây = \(\frac{{191}}{{180}}\)giờ, nên ta có:
\(\frac{x}{{12}} + \frac{y}{{3,75}} + \frac{z}{{45}} = \frac{{191}}{{180}}\)
Tổng thời gian thi đấu ba môn phối hợp của Mạnh là 1 giờ 1 phút 55 giây = \(\frac{{743}}{{720}}\)giờ, nên ta có:
\(\frac{x}{{12,5}} + \frac{y}{4} + \frac{z}{{45}} = \frac{{743}}{{720}}\)
Từ đó ta có hệ phương trình bậc nhất ba ẩn
\(\left\{ \begin{array}{l}\frac{x}{{12,5}} + \frac{y}{{3,6}} + \frac{z}{{48}} = 1,025\\\frac{x}{{12}} + \frac{y}{{3,75}} + \frac{z}{{45}} = \frac{{191}}{{180}}\\\frac{x}{{12,5}} + \frac{y}{4} + \frac{z}{{45}} = \frac{{743}}{{720}}\end{array} \right.\)
Sử dụng máy tính cầm tay, ta được \(x = 5;y = 0,75;z = 20\)
Vậy cự li chạy là 5km, cự li bơi là 0,75km và cự li đạp xe là 20km.