Câu hỏi 1 :
Ở \({20^0}C\) điện trở suất của bạc là \(1,{62.10^{ - 8}}\Omega .m.\) Hệ số nhiệt điện trở của bạc là \(4,{1.10^{ - 3}}{\mkern 1mu} {K^{ - 1}}\). Ở 330K thì điện trở suất của bạc là
- A \(1,{866.10^{ - 8}}\Omega .m\)
- B \(3,{697.10^{ - 8}}\Omega .m\)
- C \(3,{812.10^{ - 8}}\Omega .m\)
- D \(4,{151.10^{ - 8}}\Omega .m\)
Đáp án: A
Phương pháp giải:
Áp dụng công thức: \(\rho {\rm{ \;}} = {\rho _0}\left( {1 + \alpha \Delta t} \right)\)
Lời giải chi tiết:
Ta có: \({t_0} = {20^0}C \Rightarrow T = 20 + 273 = 293K\)
Điện trở suất của bạc là:
\(\rho {\rm{ \;}} = {\rho _0}\left( {1 + \alpha \Delta t} \right) = 1,{62.10^{ - 8}}.\left[ {1 + 4,{{1.10}^{ - 3}}.\left( {330 - 293} \right)} \right] = 1,{866.10^{ - 8}}\left( {\Omega .m} \right)\)
Câu hỏi 2 :
Điều kiện để có dòng điện là:
- A Có nguồn điện.
- B Có điện tích tự do.
- C Có hiệu điện thế.
- D Có hiệu điện thế và điện tích tự do.
Đáp án: D
Phương pháp giải:
Sử dụng điều kiện để có dòng điện
Lời giải chi tiết:
Điều kiện để có dòng điện là cần phải duy trì một hiệu điện thế giữa đặt vào hai đầu vật dẫn điện.
Như vậy, cần có điện tích tự do để có thể chuyển động, có hiệu điện thế để có một điện trường làm cho các điện tích tự do chịu lực điện và chuyển động thành dòng có hướng.
Câu hỏi 3 :
Khi đốt nóng chất khí, nó trở lên dẫn điện vì
- A vận tốc giữa các phân tử chất khí tăng.
- B khoảng cách giữa các phân tử chất khí tăng.
- C chất khí chuyển động thành dòng có hướng.
- D các phân tử chất khí bị ion hóa thành các hạt mang điện tự do.
Đáp án: D
Phương pháp giải:
Sử dụng kiến thức dòng điện trong chất khí.
Lời giải chi tiết:
Khi đốt nóng chất khí, nó trở nên dẫn điện là do các phân tử chất khí bị ion hóa thành các hạt mang điện tự do.
Câu hỏi 4 :
Suất điện động của một cặp nhiệt điện phụ thuộc vào
- A hiệu nhiệt độ hai đầu cặp.
- B nhiệt độ cao hơn ở một trong hai đầu cặp.
- C nhiệt độ thấp hơn ở một trong hai đầu cặp.
- D bản chất của chỉ một trong hai kim loại cấu tạo nên cặp.
Đáp án: A
Phương pháp giải:
Vận dụng biểu thức xác định suất điện động nhiệt điện: \(E = {\alpha _T}\left( {{T_1} - {T_2}} \right)\)
Lời giải chi tiết:
Ta có: Suất điện động nhiệt điện: \(E = {\alpha _T}\left( {{T_1} - {T_2}} \right)\)
→ Suất điện động nhiệt điện phụ thuộc vào hiệu nhiệt độ hai đầu cặp.
Câu hỏi 5 :
Khi vật dẫn ở trạng thái siêu dẫn, điện trở của nó
- A bằng không.
- B có giá trị âm.
- C vô cùng lớn.
- D có giá trị xác định.
Đáp án: A
Phương pháp giải:
Sử dụng lí thuyết về vật siêu dẫn.
Lời giải chi tiết:
Khi vật dẫn ở trạng thái siêu dẫn, điện trở của nó bằng không.
Câu hỏi 6 :
Cho dòng điện có cường độ 2A chạy qua bình điện phân đựng dung dịch muối đồng có cực dương bằng đồng trong 1 giờ 4 phút 20 giây. Biết khối lượng mol của đồng là 64g/mol, đồng có hóa trị 2. Khối lượng đồng bám vào cực âm là
- A 2,65g.
- B 6,25g.
- C 2,56g.
- D 5,62g.
Đáp án: C
Phương pháp giải:
Áp dụng công thức: \(m = \frac{1}{F}.\frac{A}{n}.It\)
Lời giải chi tiết:
Khối lượng đồng bám vào cực âm là:
\(m = \frac{1}{F} \cdot \frac{{AIt}}{n} = \frac{1}{{96500}} \cdot \frac{{64.2.\left( {1.3600 + 4.60 + 20} \right)}}{2} = 2,56(g)\)
Câu hỏi 7 :
Lớp vỏ nguyên tử Hidro bị mất hết electron thì nó mang điện tích là:
- A \( + 1,{6.10^{ - 19}}C\)
- B \( - 1,{6.10^{ - 19}}C\)
- C \( + 3,{2.10^{ - 19}}C\)
- D \( - 3,{2.10^{ - 19}}C\)
Đáp án: C
Phương pháp giải:
Nguyên tử trung hòa về điện
Khi nguyên tử mất electron đồng nghĩa với việc nguyên tử đó sẽ mang điện dương.
Lời giải chi tiết:
Vì nguyên tử Hidro chỉ có 1 electron nên sau khi mất electron thì nguyên tử có điện tích là:
\( + 2.1,{6.10^{ - 19}} = 3,{2.10^{ - 19}}\left( C \right)\)
Câu hỏi 8 :
Hai điện tích điểm đặt gần nhau, nếu giảm khoảng cách giữa chúng đi 2 lần thì lực tương tác giữa chúng sẽ:
- A tăng lên 2 lần.
- B giảm đi 4 lần.
- C tăng lên 4 lần.
- D giảm đi 2 lần.
Đáp án: C
Phương pháp giải:
Sử dụng công thức: \(F = \frac{{k\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)
Lời giải chi tiết:
Lực tương tác giữa hai điện tích: \(F = \frac{{k\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}} \Rightarrow F\~\frac{1}{r}\)
Khi r giảm đi 2 lần thì lực tương tác tăng 4 lần.
Câu hỏi 9 :
Đơn vị của điện thế trong hệ SI là
- A N (niuton)
- B J (Jun)
- C V (vôn)
- D m (mét)
Đáp án: C
Phương pháp giải:
Sử dụng kiến thức về đơn vị của các đại lượng.
Lời giải chi tiết:
Đơn vị của điện thế trong hệ SI là Vôn (V)
Câu hỏi 10 :
Cho đoạn mạch điện trở \(10\Omega \), hiệu điện thế hai đầu mạch là 20V. Điện năng đoạn mạch trên tiêu thụ trong 1 giờ là:
- A 2,4 kJ
- B 144 kJ.
- C 120 J.
- D 40 J.
Đáp án: B
Phương pháp giải:
Áp dụng công thức: \(A = UIt = \frac{{{U^2}}}{R}.t\)
Lời giải chi tiết:
Điện năng đoạn mạch tiêu thụ là:
\(A = \frac{{{U^2}}}{R}t = \frac{{{{20}^2}}}{{10}}.3600 = 144000{\mkern 1mu} \left( J \right) = 144\left( {kJ} \right)\)
Câu hỏi 11 :
Cho đoạn mạch như hình vẽ (Hình 1) trong đó \({E_1} = 9V,{\mkern 1mu} {\mkern 1mu} {r_1} = 1,2\Omega ;{\mkern 1mu} {\mkern 1mu} {E_2} = 3V,{\mkern 1mu} {r_2} = 0,4\Omega ;\) điện trở \(R = 28,4\Omega \). Hiệu điện thế giữa hai đầu đoạn mạch \({U_{AB}} = 6V\). Dòng điện chạy qua đoạn mạch có
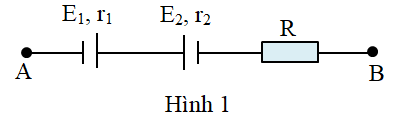
- A chiều từ A sang B, độ lớn 0,4A
- B chiều từ B sang A, độ lớn 0,4A
- C chiều từ A sang B, độ lớn 0,6A
- D chiều từ B sang A, độ lớn 0,6A
Đáp án: A
Phương pháp giải:
Áp dụng công thức định luật Ôm cho đoạn mạch chứa nguồn và máy thu.
Lời giải chi tiết:
Giả sử dòng điện trong đoạn mạch có chiều từ A đến B. Khi đó \({{\rm{E}}_1}\) là máy phát, \({{\rm{E}}_2}\) là máy thu.
Áp dụng định luật Ôm cho đoạn mạch AB, ta có:
\(I = \frac{{{U_{AB}} + {E_1} - {E_2}}}{{R + {r_1} + {r_2}}} = \frac{{6 + 9 - 3}}{{28,4 + 1,2 + 0,4}} = 0,4{\mkern 1mu} {\mkern 1mu} \left( A \right)\)
Do \(I > 0\) nên dòng điện có chiều từ A đến B
Câu hỏi 12 :
Khi nói về chất điện môi, phát biểu nào sau đây không đúng?
- A Hằng số điện môi của một môi trường xác định là hằng số.
- B Điện môi là môi trường cách điện.
- C Hằng số điện môi có thể nhỏ hơn 1.
- D Hằng số điện môi của chân không bằng 1.
Đáp án: C
Phương pháp giải:
Sử dụng lí thuyết về điện môi, hằng số điện môi
Lời giải chi tiết:
- Điện môi là một môi trường cách điện.
- Hằng số điện môi \(\varepsilon \ge 1\)
- Đối với chân không \(\varepsilon = 1,\) còn đối với các môi trường khác \(\varepsilon > 1\)
\( \Rightarrow \) Hằng số điện môi không thể nhỏ hơn 1.
Câu hỏi 13 :
Công của lực điện trường dịch chuyển một điện tích \(1\mu C\) dọc theo chiều một đường sức trong một điện trường đều 1000 V/m trên quãng đường dài 1m là
- A 1 J.
- B 1 mJ.
- C 1000 J.
- D \(1{\mkern 1mu} {\mkern 1mu} \mu {\rm{J}}.\)
Đáp án: B
Phương pháp giải:
Áp dụng công thức: \(A = qEd\)
Lời giải chi tiết:
Công của lực điện làm điện tích di chuyển là:
\(A = qEd = {1.10^{ - 6}}.1000.1 = {10^{ - 3}}{\mkern 1mu} \left( J \right) = 1{\mkern 1mu} \left( {mJ} \right)\)
Câu hỏi 14 :
Một electron được thả không vận tốc ban đầu ở sát bản âm trong điện trường đều giữa hai bản kim loại phẳng tích điện trái dấu. Cường độ điện trường giữa hai bản là 100 V/m. Khoảng cách giữa hai bản là 1cm. Động năng của electron khi nó đến đập vào bản dương là
- A \(1,{6.10^{ - 17}}J.\)
- B \(1,{6.10^{ - 19}}{\mkern 1mu} J\)
- C \(1,{6.10^{ - 20}}{\mkern 1mu} J\)
- D \(1,{6.10^{ - 18}}{\mkern 1mu} J\)
Đáp án: D
Phương pháp giải:
Áp dụng công thức định lí động năng: \({{\rm{W}}_d} - 0 = qEd\)
Lời giải chi tiết:
Điện trường giữa hai bản là điện trường đều E = 1000 V/m.
Lực điện trường F tác dụng lên electron (điện tích âm) có chiều ngược với chiều điện trường do đó electron di chuyển ngược chiều điện trường \( \Rightarrow \left( {\vec E;\vec s} \right) = {180^0}\)
Áp dụng định lý động năng cho sự di chuyển của êlectron:
\({{\rm{W}}_d} - 0 = qEd \Rightarrow {{\rm{W}}_d} = - 1,{6.10^{ - 19}}.1000.\left( { - {{1.10}^{ - 2}}} \right) = 1,{6.10^{ - 18}}{\mkern 1mu} {\mkern 1mu} \left( J \right)\)
Câu hỏi 15 :
Điện năng tiêu thụ được đo bằng dụng cụ nào sau đây?
- A Tĩnh điện kế.
- B Vôn kế.
- C Ampe kế.
- D Công tơ điện.
Đáp án: D
Phương pháp giải:
Sử dụng lí thuyết về công dụng của các dụng cụ đo.
Lời giải chi tiết:
Tĩnh điện kế: dùng để đo điện tích hoặc điện thế.
Vôn kế: Dùng để đo điện thế, hiệu điện thế.
Ampe kế: Dùng để đo cường độ dòng điện.
Công tơ điện: Dùng để đo điện năng tiêu thụ.
Câu hỏi 16 :
Hiện tượng điện phân không ứng dụng để
- A đúc điện.
- B mạ điện.
- C sơn tĩnh điện.
- D luyện nhôm
Đáp án: C
Phương pháp giải:
Sử dụng ứng dụng của hiện tượng điện phân
Lời giải chi tiết:
Hiện tượng điện phân ứng dụng để đúc điện, mạ điện, luyện nhôm ... không dùng để sơn tĩnh điện
Câu hỏi 17 :
Để bóng đèn loại 120V–60W sáng bình thường, người ta phải mắc bóng đèn đó ở mạng điện có hiệu điện thế là
- A 20V.
- B 120V.
- C 60V.
- D 100V.
Đáp án: B
Phương pháp giải:
Các thiết bị điện hoạt động bình thường khi hiệu điện thế đặt vào 2 đầu thiết bị bằng hiệu điện thế định mức.
Lời giải chi tiết:
Hiệu điện thế định mức của đèn là 120V nên để đèn sáng bình thường thì phải mắc bóng đèn vào mạng điện có hiệu điện thế 120V.
Câu hỏi 18 :
Trên vỏ một tụ điện có ghi \(20\mu F,\) số liệu đó cho biết
- A Điện dung của tụ.
- B điện tích cực đại của tụ.
- C hiệu điện thế hai đầu tụ.
- D điện tích của tụ.
Đáp án: A
Phương pháp giải:
Sử dụng đơn vị của tụ điện.
Lời giải chi tiết:
Ta thấy: đơn vị của tụ điện là Fara (F), ngoài ra còn các đơn vị \(\mu F,{\mkern 1mu} mF,pF...\)
Con số \(20\mu F\) cho biết điện dung của tụ.
Câu hỏi 19 :
Một mạch điện kín gồm hai nguồn điện \({E_1},{r_1}\) và \({E_2},{r_2}\) mắc nối tiếp với nhau, mạch ngoài chỉ có điện trở R. Biểu thức cường độ dòng điện chạy trong mạch được tính theo công thức là
- A \(I = \frac{{{E_1} - {E_2}}}{{R + {r_1} - {r_2}}}\)
- B \(I = \frac{{{E_1} - {E_2}}}{{R + {r_1} + {r_2}}}\)
- C \(I = \frac{{{E_1} + {E_2}}}{{R + {r_1} - {r_2}}}\)
- D \(I = \frac{{{E_1} + {E_2}}}{{R + {r_1} + {r_2}}}\)
Đáp án: D
Phương pháp giải:
Áp dụng công thức mắc nguồn điện thành bộ và công thức định luật ôm cho toàn mạch.
Lời giải chi tiết:
Mạch gồm 2 nguồn nối tiếp nên ta có: \(\left\{ {\begin{array}{*{20}{l}}{{E_b} = {E_1} + {E_2}}\\{{r_b} = {r_1} + {r_2}}\end{array}} \right.\)
Cường độ dòng điện trong mạch là: \(I = \frac{{{E_b}}}{{R + {r_b}}} = \frac{{{E_1} + {E_2}}}{{R + {r_1} + {r_2}}}\)
Câu hỏi 20 :
Một dòng điện không đổi. Sau 1 phút có một điện lượng 24C chuyển qua một tiết diện thẳng. Cường độ của dòng điện đó là
- A 24A
- B 2,4A
- C 0,2A
- D 0,4A
Đáp án: D
Phương pháp giải:
Áp dụng công thức: \(q = It \Rightarrow I = \frac{q}{t}\)
Lời giải chi tiết:
Cường độ của dòng điện là: \(I = \frac{q}{t} = \frac{{24}}{{60}} = 0,4\left( A \right)\)
Câu hỏi 21 :
Khi ánh sáng truyền từ môi trường có chiết suất lớn sang môi trường có chiết suất nhỏ hơn thì
- A không thể có hiện tượng phản xạ toàn phần
- B có thể xảy ra hiện tượng phản xạ toàn phần
- C hiện tượng phản xạ toàn phần xảy ra khi i < igh
- D luôn luôn xảy ra hiện tượng phản xạ toàn phần
Đáp án: B
Phương pháp giải:
Hiện tượng phản xạ toàn phần xảy ra khi ánh sáng truyền từ môi trường chiết suất lớn sang môi trường có chiết suất nhỏ với góc tới i > igh
Lời giải chi tiết:
Khi ánh sáng truyền từ môi trường có chiết suất lớn sang môi trường có chiết suất nhỏ hơn thì có thể xảy ra hiện tượng phản xạ toàn phần
Câu hỏi 22 :
Một tia sáng truyền từ môi trường A vào môi trường B dưới góc tới 90 thì góc khúc xạ là 80. Tính vận tốc ánh sáng trong môi trường A. Biết vận tốc ánh sáng trong môi trường B là 2.105 km/s.
- A 2,25.105 km/s.
- B 2,3.105 km/s.
- C 1,8.105 km/s.
- D 2,5.105 km/s.
Đáp án: A
Phương pháp giải:
Định luật khúc xạ ánh sáng: n1sini = n2sinr
Vận tốc ánh sáng truyền trong các môi trường liên hệ với nhau: n1/n2 = v2/v1
Lời giải chi tiết:
Theo định luật khúc xạ ánh sáng: n1sin90 = n2sin80 => n1/n2 = 0,89
Mà v2 = 2.105km/s => v1 = v2n2/n1 = 2.105/0,89 = 2,25.105km/s
Câu hỏi 23 :
Một chùm tia song song hẹp truyền trong không khí tới gặp mặt thoáng của một chất lỏng có chiết suất n với góc tới i = 60° ta có tia phản xạ vuông góc với tia khúc xạ. Góc lệch của tia sáng đi vào chất lỏng là
- A 15°
- B 45°
- C 30°
- D 60°
Đáp án: C
Phương pháp giải:
Định luật phản xạ ánh sáng: i = i’
Định luật khúc xạ ánh sáng: n1sini = n2sinr
Lời giải chi tiết:
Do i = i’; tia phản xạ và khúc xạ vuông góc nên i + r = 900 => r = 300
Góc lệch của tia sáng: D = i– r = 600 – 300 = 300
Câu hỏi 24 :
Một người nhìn hòn sỏi dưới đáy một bể nước thấy ảnh của nó dường như cách mặt nước một khoảng 120cm. Chiết suất của nước là n = \(\frac{4}{3}\). Độ sâu của bể nước là
- A 10cm
- B 16cm
- C 16dm
- D 100cm
Đáp án: C
Phương pháp giải:
Định luật khúc xạ ánh sáng: n1sini = n2sinr
Với góc nhỏ thì sini ≈ tani ≈i
Lời giải chi tiết:
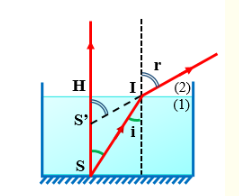
Gọi S là hòn sỏi dưới đáy bể, S’ là ảnh của S. Để ảnh rõ nét thì góc tới phải nhỏ
Ta có: \(\frac{{\sin i}}{{{\mathop{\rm s}\nolimits} {\rm{inr}}}} = \frac{{{n_2}}}{{{n_1}}}(1)\)
Mà \(\tan i = \frac{{HI}}{{HS}};{\mathop{\rm t}\nolimits} {\rm{anr}} = \frac{{HI}}{{HS'}} \Rightarrow \frac{{\tan i}}{{{\mathop{\rm t}\nolimits} {\rm{anr}}}} = \frac{{HS'}}{{HS}}(2)\)
Vì góc tới nhỏ nên sini ≈ tani ≈i
Từ (1) và (2) ta được \(\frac{{{n_2}}}{{{n_1}}} = \frac{{HS'}}{{HS}} \Rightarrow HS = \frac{{{n_1}}}{{{n_2}}}HS' = 1,6m = 16dm\)
Câu hỏi 25 :
Ánh sáng truyền trong môi trường có chiết suất n1, tới mặt phân cách với môi trường có chiết suất n2 với góc tới i ≠ 0. Xét các điều kiện sau:
(1) n2 > n1 (2) n2 < n1 (3) sini ≥ n2/n1 (3) sini ≤ n2/n1
Nếu muốn có phản xạ toàn phần thì (các) điều kiện là
- A (1).
- B (2).
- C (1) và (4).
- D (2) và (3).
Đáp án: D
Phương pháp giải:
Hiện tượng phản xạ toàn phần xảy ra khi ánh sáng truyền từ môi trường chiết suất lớn sang môi trường có chiết suất nhỏ với góc tới i > igh
Với igh = n2/n1
Lời giải chi tiết:
Hiện tượng phản xạ toàn phần xảy ra khi ánh sáng truyền từ môi trường chiết suất lớn sang môi trường có chiết suất nhỏ với góc tới i > igh
Với igh = n2/n1
Câu hỏi 26 :
Một tia sáng truyền trong hai môi trường theo đường truyền như hình vẽ. Chỉ ra câu sai.
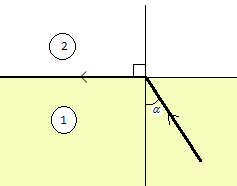
- A α là góc tới giới hạn
- B Với i > α sẽ có phản xạ toàn phần
- C Nếu ánh sáng truyền từ (2) tới (1) chỉ có phản xạ thông thường
- D Nếu ánh sáng truyền từ (2) tới (1) không thể có phản xạ
Đáp án: D
Phương pháp giải:
Định luật khúc xạ ánh sáng n1sini = n2sinr
Hiện tượng phản xạ toàn phần xảy ra khi ánh sáng truyền từ môi trường chiết suất lớn sang môi trường có chiết suất nhỏ với góc tới i > igh
Với igh = n2/n1
Lời giải chi tiết:
Định luật khúc xạ ánh sáng n1sinα= n2sin90 = n2 => n2< n1
Nếu ánh sáng truyền từ (2) tới (1) không thể có phản xạ
Câu hỏi 27 :
Chiếu một tia sáng đơn sắc từ chân không vào một khối chất trong suốt với góc tới 450 thì góc khúc xạ bằng 300. Chiết suất tuyệt đối của môi trường này là
- A \(\sqrt 3 \)
- B 1,33.
- C \(\sqrt[{}]{2}\).
- D 1,5
Đáp án: C
Phương pháp giải:
Định luật khúc xạ ánh sáng n1sini = n2sinr
Lời giải chi tiết:
Định luật khúc xạ ánh sáng n1sini = n2sinr
=> 1.sin450 = n.sin300 => n = \(\sqrt[{}]{2}\)
Câu hỏi 28 :
Một người thợ săn cá nhìn con cá dưới nước theo phương thẳng đứng. Cá cách mặt nước 40 cm, mắt người cách mặt nước 60 cm. Chiết suất của nước là \(\frac{4}{3}\). Mắt người nhìn thấy ảnh của con cá cách mắt một khoảng là
- A 95 cm.
- B 85 cm.
- C 80 cm.
- D 90 cm
Đáp án: D
Phương pháp giải:
Định luật khúc xạ ánh sáng: n1sini = n2sinrVới góc nhỏ thì sini ≈ tani ≈i
Lời giải chi tiết:
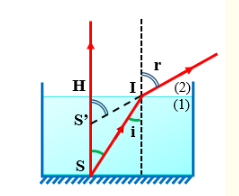
Gọi S là hòn con cá, S’ là ảnh của con cá. Để ảnh rõ nét thì góc tới phải nhỏ
Ta có: \(\frac{{\sin i}}{{{\mathop{\rm s}\nolimits} {\rm{inr}}}} = \frac{{{n_2}}}{{{n_1}}}(1)\)
Mà \(\tan i = \frac{{HI}}{{HS}};{\mathop{\rm t}\nolimits} {\rm{anr}} = \frac{{HI}}{{HS'}} \Rightarrow \frac{{\tan i}}{{{\mathop{\rm t}\nolimits} {\rm{anr}}}} = \frac{{HS'}}{{HS}}(2)\)
Vì góc tới nhỏ nên sini ≈ tani ≈i
Từ (1) và (2) ta được \(\frac{{{n_2}}}{{{n_1}}} = \frac{{HS'}}{{HS}} \Rightarrow HS' = \frac{{{n_2}}}{{{n_1}}}HS = 30cm\)
Vậy mắt người thấy cá cách mình 30 + 60 = 90cm
Câu hỏi 29 :
Một lăng kính có tiết diện thẳng là tam giác đều, ba mặt như nhau, chiết suất n = \(\sqrt 3 \), được đặt trong không khí. Chiếu tia sáng đơn sắc nằm trong mặt phẳng tiết diện thẳng, vào mặt bên của lăng kính với góc tới i= 600. Góc lệch D của tia ló và tia tới bằng
- A 600
- B 450
- C 300
- D 900
Đáp án: A
Phương pháp giải:
Góc lệch D = i1 + i2 – A
Với i1 = nr1; i2 = nr2, r1 + r2 = A
Định luật khúc xạ ánh sáng: n1sini = n2sinr
Lời giải chi tiết:
Ta có sini1 = nsinr1 => r1 = 300 => r2 = 300 => i2 = 600
Góc lệch D = i1 + i2 – A = 600
Câu hỏi 30 :
Lăng kính có góc chiết quang A = 300 và chiết suất n = \(\sqrt 2 \). Tia ló truyền thẳng ra không khí vuông góc với mặt thứ hai của lăng kính khi góc tới i1 có giá trị:
- A 300.
- B 600.
- C 450.
- D 350
Đáp án: C
Phương pháp giải:
Góc lệch D = i1 + i2 – A
Với sini1 = nsinr1; sini2 = nsinr2, r1 + r2 = A
Định luật khúc xạ ánh sáng: n1sini = n2sinr
Lời giải chi tiết:
Tia ló truyền thẳng ra không khí vuông góc với mặt thứ hai của lăng kính => i2 = 0
Ta có: sini2 = nsinr2 => r2 = 0 => r1 = A =300
Mà sini1 = nsinr1 => sini1 = \(\sqrt 2 \) sin300 => i1 = 450
Câu hỏi 31 :
Một vật sáng AB đặt vuông góc với trục chính của một thấu kính hội tụ có tiêu cự f cho ảnh thật cách thấu kính một đọan d’= 2f . Khi đó khoảng cách từ vật tới ảnh là
- A 2f.
- B 3f.
- C 5f.
- D 4f
Đáp án: A
Phương pháp giải:
Công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\)
Lời giải chi tiết:
Công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\)
Theo đề bài ta có: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{2f}} \Rightarrow d = 2f\)
Câu hỏi 32 :
Một lăng kính có chiết suất n, đặt trong không khí, có góc chiết quang A, nhận một tia sáng tới vuông góc với mặt bên AB và tia ló sát mặt bên AC của lăng kính. Chiết suất n của lăng kính xác định bởi
- A n = \(\frac{1}{{\sin A}}\)
- B n = sini
- C n = sinA
- D n = \(\frac{1}{{\sin (A + i)}}\)
Đáp án: A
Phương pháp giải:
Góc lệch D = i1 + i2 – A
Với sini1 = nsinr1; sini2 = nsinr2, r1 + r2 = A
Định luật khúc xạ ánh sáng: n1sini = n2sinr
Lời giải chi tiết:
Theo đề bài ta có i = 00, i’ = 900
Sini1 = nsinr1 => r1= 0 => r2 = A
Sini2 = nsinr2 = nsinA => n = \(\frac{1}{{\sin A}}\)
Câu hỏi 33 :
Chọn phát biểu đúng với vật thật đặt trước thấu kính.
- A Thấu kính hội tụ luôn tạo chùm tia ló hội tụ
- B Thấu kính phân kì luôn tạo chùm tia ló phân kì
- C Ảnh của vật tạo bởi thấu kính không thể bằng vật
- D Ảnh của vật qua thấu kính phân kì là ảnh thật
Đáp án: B
Phương pháp giải:
Thấu kính phân kì luôn tạo chùm tia ló phân kì
Lời giải chi tiết:
Thấu kính phân kì luôn tạo chùm tia ló phân kì
Câu hỏi 34 :
Vật sáng đặt trước một thấu kính hội tụ có tiêu cự f, cách thấu kính một khỏang D. Nếu d>f , bao giờ cũng có ảnh
- A luôn nhỏ hơn vật.
- B cùng kích thước với vật.
- C ảo.
- D ngược chiều với vật.
Đáp án: D
Phương pháp giải:
Với thấu kính hội tụ, vật nằm ngoài khoảng tiêu cự luôn cho ảnh thật, ngược chiều vật.
Lời giải chi tiết:
Với thấu kính hội tụ, vật nằm ngoài khoảng tiêu cự luôn cho ảnh thật, ngược chiều vật.
Câu hỏi 35 :
Vị trí của vật và ảnh cho bởi thấu kính L trường hợp nào sau đây là sai?
- A Cho vật tiến lại gần L, ảnh di chuyển cùng chiều với vật
- B Cho vật tiến ra xa L, ảnh di chuyển ngược chiều với vật
- C Vật ở rất xa thì ảnh ở tiêu diện ảnh
- D Ảnh ở rất xa thì vật ở tiêu diện vật
Đáp án: B
Phương pháp giải:
Ảnh tạo bởi thấu kính dịch chuyển cùng chiều với vật
Lời giải chi tiết:
Ảnh tạo bởi thấu kính dịch chuyển cùng chiều với vật
Vậy nên nói Cho vật tiến ra xa L, ảnh di chuyển ngược chiều với vật là sai.
Câu hỏi 36 :
Vật sáng phẳng, nhỏ AB đặt vuông góc với trục chính của một thấu kính có tiêu cự f = 30 cm. Qua thấu kính vật cho một ảnh thật có chiều cao gấp 2 lần vật. Khoảng cách từ vật đến thấu kính
- A 60cm
- B 45cm
- C 30cm
- D 20cm
Đáp án: B
Phương pháp giải:
Công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\)
Hệ số phóng đại k = d’/d = h’/h
Lời giải chi tiết:
Vì ảnh thật cao gấp 2 lần vật nên d’ = 2d
Công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}} \Rightarrow \frac{1}{{30}} = \frac{1}{d} + \frac{1}{{2d}} = \frac{3}{{2d}} \Rightarrow d = 45cm\)
Câu hỏi 37 :
Thấu kính hội tụ có tiêu cự 5 cm. A là điểm vật thật trên trục chính, cách thấu kính 10 cm, A’ là ảnh của A. Tính khoảng cách AA’.
- A 16 cm.
- B 24cm
- C 10cm
- D 20cm
Đáp án: D
Phương pháp giải:
Công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\)
Lời giải chi tiết:
Công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}} \Rightarrow \frac{1}{5} = \frac{1}{{10}} + \frac{1}{{d'}} \Rightarrow d' = 10cm\)
Khoảng cách AA’ là d + d’ = 10 + 10 = 20cm
Câu hỏi 38 :
Một vật sáng phẳng AB có chiều cao H đặt vuông góc với trục chính của thấu kính và ở trước thấu kính. Khi di chuyển thấu kính giữa vật và màn, có hai vị trí cho ảnh rõ nét trên màn. Các ảnh trên màn có chiều cao lần lượt là h1 và h2. Khoảng cách giữa vật sáng và màn ảnh không đổi. Chiều cao H tính theo h1 và h2 là:
- A \(H = \sqrt {{h_1} + {h_2}} \)
- B \(H = \sqrt {{h_1}{h_2}} \)
- C \(H = \frac{{{h_1}}}{{{h_2}}}\)
- D \(H = \frac{{{h_1}}}{{{h_1} + {h_2}}}\)
Đáp án: B
Phương pháp giải:
Công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\)
Hệ số phóng đại k = h’/h = d’/d
Lời giải chi tiết:
Công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}} \Rightarrow d' = \frac{{df}}{{d - f}} \Rightarrow d + d' = \frac{{{d^2}}}{{d - f}} = L \Rightarrow d{}^2 - dL + fL = 0\)
Do f không đổi nên có 2 vị trí thấu kính cho ảnh rõ nét trên màn nên d là nghiệm của phương trình bậc 2 trên
\({d_1} = \frac{{d + \sqrt {{L^2} - 4fL} }}{2};{d_2} = \frac{{d - \sqrt {{L^2} - 4fL} }}{2}\)
Ta có: \(\frac{{{h_1}}}{h} = \frac{{{d_1}'}}{{{d_1}}} = \frac{f}{{{d_1} - f}};\frac{{{h_2}}}{h} = \frac{{{d_2}'}}{{{d_2}}} = \frac{f}{{{d_2} - f}} \Rightarrow \frac{{{h_1}{h_2}}}{{{h^2}}} = 1 \Rightarrow h = \sqrt {{h_1}{h_2}} \)
Câu hỏi 39 :
Vật sáng phẳng AB đặt vuông góc với trục chính của một thấu kính cho ảnh lớn gấp 3 lần vật. Khi dịch chuyển vật gần thêm một khoảng 8 cm thì thấy ảnh có độ lớn không đổi. Tính tiêu cự của thấu kính.
- A 10cm
- B 20cm
- C 12cm
- D 30cm
Đáp án: C
Phương pháp giải:
Công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\)
Hệ số phóng đại k = h’/h = d’/d
Lời giải chi tiết:
Ảnh lớn gấp 3 lần vật nên d’ = 3d, h’ = 3h. Ta có: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{3d}} = \frac{4}{{3d}} \Rightarrow f = \frac{{3d}}{4}\)
Khi dịch chuyển vật lại gần 8cm thì d1 = d – 8, ảnh có độ lớn không đổi nên h’ = 3h => d1’ = 3(d-8)
Ta có: \(\frac{1}{f} = \frac{1}{{d - 8}} + \frac{1}{{3(d - 8)}} = \frac{4}{{3d}} \Rightarrow d = 16cm \Rightarrow f = 12cm\)
Câu hỏi 40 :
Mắt của một người có điểm cực viễn cách mắt 50 cm. Mắt người này
- A không có tật
- B bị tật cận thị
- C bị tật lão thị
- D bị tật viễn thị
Đáp án: B
Phương pháp giải:
Mắt tốt có điểm cực viễn ở xa vô cực. Người có cực viễn không ở xa vô cực là bị tật cận thị.
Lời giải chi tiết:
Mắt tốt có điểm cực viễn ở xa vô cực. Người có cực viễn cách mắt 50cm nên bị tật cận thị.
Câu hỏi 41 :
Trường hợp nào dưới đây, mắt nhìn thấy vật ở xa vô cực?
- A Mắt không có tật, không điều tiết
- B Mắt không có tật và điều tiết tối đa
- C Mắt cận không điều tiết
- D Mắt viễn không điều tiết
Đáp án: A
Phương pháp giải:
Mắt tốt có điểm cực viễn ở xa vô cực khi không điều tiết.
Lời giải chi tiết:
Mắt tốt có điểm cực viễn ở xa vô cực khi không điều tiết.
Câu hỏi 42 :
Một người cận thị phải đeo sát mắt một kính có độ tụ - 4dp, nhìn rõ được các vật ở vô cực. Điểm cực viễn của mắt người ấy khi không đeo kính cách mắt một khoảng là
- A OCV = 40cm
- B OCV = 4cm
- C OCV = 25cm
- D OCV = 400cm
Đáp án: C
Phương pháp giải:
Người bị tật cận thị phải đeo kính phân kỳ có tiêu cự bằng khoảng cực viễn
Độ tụ của kính D = 1/f
Lời giải chi tiết:
Tiêu cự kính phân kỳ người đó phải đeo là f = 1/D = - 0,25m
Vậy điểm cực viễn khi không đeo kính cách mắt 0,25m = 25cm
Câu hỏi 43 :
Một người viễn thị có điểm cực cận cách mắt 40cm. Để có thể nhìn thấy vật gần nhất cách mắt 25cm, người đó cần đeo sát mắt một kính có độ tụ bằng
- A 1,5 điôp.
- B - 1,5 điôp.
- C - 1,25 điôp.
- D 1,25 điôp.
Đáp án: A
Phương pháp giải:
Để nhìn được vật gần nhất thì vật đó phải cho ảnh ở điểm cực cận.
Công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\)
Lời giải chi tiết:
Công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\)
Khi d = 25cm thì d’ = - 40cm \( \Rightarrow \frac{1}{f} = \frac{1}{{0,25}} - \frac{1}{{0,40}} = 1,5dp\)
Câu hỏi 44 :
Một học sinh bố trí thí nghiệm theo sơ đồ như hình vẽ. Thấu kính phân kì L có tiêu cự -10 cm. Khoảng cách từ ảnh tạo bởi thấu kính đến màn có giá trị nào?
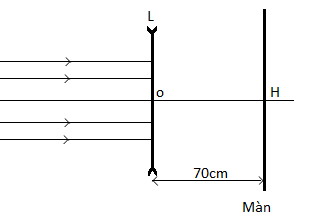
- A 60cm
- B 70cm
- C 80cm
- D 100cm
Đáp án: C
Phương pháp giải:
Công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\)
Lời giải chi tiết:
Theo bài ra: d = ∞ nên cho ảnh tại tiêu điểm => d’ = f = -10cm
Khoảng cách từ ảnh đến màn là 10 + 70 = 80cm
Câu hỏi 45 :
Khi chiếu tia sáng đơn sắc qua lăng kính có tiết diện là tam giác đều với góc tới i1 = 450 thì góc khúc xạ r1 bằng góc tới r2 (hình vẽ). Góc lệch của tia sáng qua lăng kính khi đó là
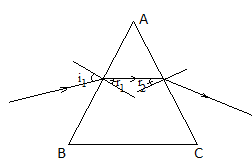
- A 450
- B 300
- C 900
- D 600
Đáp án: B
Phương pháp giải:
Góc lệch D = i1 + i2 – A
Với sini1 = nsinr1; sini2 = nsinr2, r1 + r2 = A
Định luật khúc xạ ánh sáng: n1sini = n2sinr
Lời giải chi tiết:
Ta có r1 + r2 = 2r1 = A = 600 => r1 = 300
Sini1 = nsinr1 => n = \(\sqrt 2 \)
nsinr2 = sini2 => \(\sqrt 2 \)sin300 = sini2 => i2 = 450
Góc lệch : D = i1 + i2 – A = 45 + 45 – 60 = 30
