Đề bài
Cho \(\widehat {xAy} = {55^ \circ }.\) Từ điểm C nằm trong góc đó vẽ \(CB \bot Ax\left( {B \in Ax} \right),CD \bot Ay\left( {D \in Ay} \right)\)
a) Tính số đo \(\widehat {BCD}\) .
b) Tính các góc ngoài của tứ giác tại đỉnh B và đỉnh C.
Phương pháp giải - Xem chi tiết
Sử dụng:
Tổng bốn góc trong một tứ giác bằng \(360^0\)
Hai góc kề bù có tổng số đo bằng \(180^0\)
Lời giải chi tiết
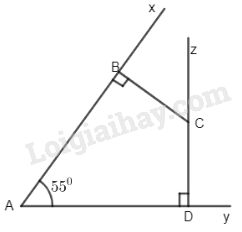
a) Ta có: \(\widehat A + \widehat B + \widehat C + \widehat D = {360^ \circ }\) (Tổng các góc của tứ giác ABCD)
\( \Rightarrow \widehat C = {360^ \circ } - \left( {\widehat A + \widehat B + \widehat D} \right) \)\(\,= {360^ \circ } - \left( {{{55}^ \circ } + {{90}^ \circ } + {{90}^ \circ }} \right) = {125^ \circ }.\)
b) Ta có :
\(\widehat {xBC} + \widehat {ABC} = {180^ \circ } \) (hai góc kề bù)
\(\Rightarrow \widehat {xBC} = {180^ \circ } - \widehat {ABC} \)\(\,= {180^ \circ } - {90^ \circ } = {90^ \circ }\)
\(\widehat {zCB} +\widehat {BCD}= {180^ \circ } \) (hai góc kề bù)
\(\Rightarrow \widehat {zCB} = {180^ \circ } - \widehat {BCD} \)\(\,= {180^ \circ } - {125^ \circ } = {55^ \circ }.\)
soanvan.me
