Đề bài
Bài 1. Tính (không dùng bảng số và máy tính):
\(A = {\sin ^2}15^\circ + {\sin ^2}75^\circ + \tan 23^\circ\)\(\; - \cot 67^\circ - {{\cot 37^\circ } \over {\tan 53^\circ }}\)
Bài 2. Cho \(∆ABC\) nhọn có \(BC = a, CA = b, AB = c\). Chứng minh rằng:
\({a \over {\sin A}} = {b \over {\sin B}} = {c \over {\sin C}}\)
LG bài 1
Phương pháp giải:
Sử dụng: Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
Và \(\sin^2\alpha +\cos^2\alpha =1\)
Lời giải chi tiết:
Ta có:
\(\eqalign{ & {\sin ^2}75^\circ = {\cos ^2}\left( {90^\circ - 75^\circ } \right) = {\cos ^2}15^\circ \cr & \cot 67^\circ = \tan \left( {90^\circ - 67^\circ } \right) = \tan 23^\circ \cr & \cot 37^\circ = \tan \left( {90^\circ - 37^\circ } \right) = \tan 53^\circ \cr} \)
Vậy \(A = {\sin ^2}15^\circ + {\cot ^2}15^\circ + \tan 23^\circ \)\(\, - \tan 23^\circ - {{\tan 53^\circ } \over {\tan 53^\circ }} = 1 - 1 = 0\)
LG bài 2
Phương pháp giải:
Sử dụng: Cho tam giác ABC vuông tại A ta có: \(\sin B=\dfrac{AC}{BC};\cos B=\dfrac{AB}{BC}\)
Lời giải chi tiết:
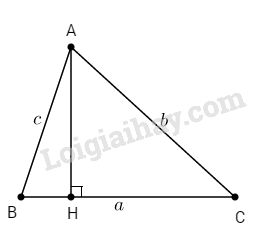
Kẻ đường cao AH, ta có: \(\sin B = {{AH} \over {AB}};\sin C = {{AH} \over {AC}}\)
\(\eqalign{ & \Rightarrow {{\sin B} \over {\sin C}} = {{AH} \over {AB}}:{{AH} \over {AC}} = {{AC} \over {AB}} = {b \over c} \cr & \Rightarrow {b \over {\sin B}} = {c \over {\sin C}} \cr} \)
Tương tự : \({a \over {\sin A}} = {b \over {\sin B}}\)
Từ đó ta có: \({a \over {\sin A}} = {b \over {\sin B}} = {c \over {\sin C}}\)
soanvan.me
