Đề bài
Cho tam giác nhọn ABC, các đường cao AH, BK và CI.
a. Chứng minh rằng: \(AI.BH.CK \)\(\,= AB.BC.CA.\cos A.\cos B.\cos C\)
b. Cho \(\widehat A = 60^\circ \) và \({S_{ABC}} = 160c{m^2}.\) Tính \({S_{AIK}}\)
Phương pháp giải - Xem chi tiết
Sử dụng:
Trong một tam giác vuông, mỗi cạnh góc vuông bằng: Cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề.
Tỉ số diện tích của hai tam giác đồng dạng bằng bình phương tỉ số đồng dạng.
Lời giải chi tiết
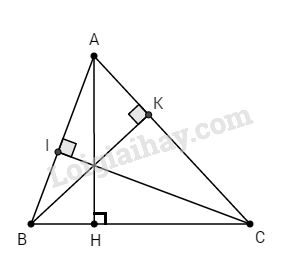
a. Ta có: \(∆AIC\) vuông tại I:
\(AI = AC.\cos A\)
Tương tự các tam giác AHB, BKC vuông,
ta có: \(BH = AB.\cos B; CK = BC.\cos C\)
Do đó: \(AI.BH.CK \)\(\,= AB.BC.CA.\cos A.\cos B.\cos C\).
b. Tam giác AKB đồng dạng với tam giác AIC (g-g) (do có góc A chung và \(\widehat I = \widehat K = {90^0}\))
Suy ra \(\frac{{AK}}{{AB}} = \frac{{AI}}{{AC}}\)
Kết hợp với góc A chung suy ra \(∆AIK\) đồng dạng \(∆ACB\) (c.g.c)
\( \Rightarrow {{{S_{AIK}}} \over {{S_{ACB}}}} = {\left( {{{AK} \over {AB}}} \right)^2}\)
\(∆AKB\) vuông tại K có \(\widehat A = 60^\circ \) (gt) \( \Rightarrow {{AK} \over {AB}} = {1 \over 2}\)
Vậy: \({{{S_{AIK}}} \over {{S_{ACB}}}} = {\left( {{1 \over 2}} \right)^2} = {1 \over 4} \)
\(\Rightarrow {S_{AIK}} = {{{S_{ACB}}} \over 4} = {{160} \over 4} = 40\,\left( {c{m^2}} \right)\)
soanvan.me
