Câu hỏi 1 :
Phát biểu nào sau đây là đúng? Trong một hệ kín
- A
các vật trong hệ chỉ tương tác với nhau.
- B
động lượng của hệ không bảo toàn
- C
tổng ngoại lực tác dụng lên các vật trong hệ khác không.
- D
nội lực và ngoại lực cân bằng nhau.
Đáp án: A
Lời giải chi tiết:
A - đúng
B – sai vì: Trong hệ kín, động lượng của hệ được bảo toàn
C – sai vì: Trong hệ kín không có ngoại lực tác dụng hoặc các hợp các ngoại lực tác dụng lên vật bằng 0
D - sai
Câu hỏi 2 :
Xét một quá trình đẳng tích của một lượng khí lí tưởng nhất định. Tìm phát biểu sai.
- A
Độ biến thiên của áp suất tỉ lệ thuận với độ biến thiên của nhiệt độ.
- B
Áp suất tỉ lệ thuận với nhiệt độ tuyệt đối.
- C
Độ biến thiên của áp suất tỉ lệ thuận với độ biến thiên của nhiệt độ Celsius.
- D
Áp suất tỉ lệ thuận với nhiệt độ Celsius.
Đáp án: D
Phương pháp giải:
Vận dụng biểu thức định luật Sáclơ
Lời giải chi tiết:
A, B, C - đúng
D - sai vì: \(p \sim T\)
Câu hỏi 3 :
Số \({6,02.10^{23}}\) là:
- A
Số phân tử (hoặc số nguyên tử) trong 1 lít khí nằm tại các điều kiện bình thường (00C và 760 mmHg).
- B
Số phân tử trong 1 mol khí.
- C
Số phân tử trong 1 cm3 khí tại các điều kiện bình thường.
- D
Số phân tử khí trong 22,4 cm3 khí tại các điều kiện bình thường.
Đáp án: B
Phương pháp giải:
Xem lí thuyết các công thức xác định các đại lượng cơ bản của chất khí
Lời giải chi tiết:
- Số Avôgađrô NA: là số nguyên tử có trong 1 mol lượng chất bất kỳ.
\({N_A} = {6,022.10^{23}}(mo{l^{ - 1}})\)
Câu hỏi 4 :
Chất điểm M chuyển động không vận tốc đầu dưới tác dụng của lực không đổi \(\overrightarrow F \).Động lượng chất điểm ở thời điểm t là:
- A
\(\overrightarrow p = \overrightarrow F m\)
- B
\(\overrightarrow p = \overrightarrow F t\)
- C
\(\overrightarrow p = \frac{{\overrightarrow F }}{m}\)
- D
\(\overrightarrow p = \frac{{\overrightarrow F }}{t}\)
Đáp án: B
Phương pháp giải:
Vận dụng biểu thức tính độ biến thiên động lượng: \(\overrightarrow {{p_2}} - \overrightarrow {{p_1}} = \Delta \overrightarrow p = \overrightarrow F \Delta t\)
Lời giải chi tiết:
Ta có: Độ biến thiên động lượng của một vật trong một khoảng thời gian nào đó bằng xung lượng của tổng các lực tác dụng lên vật trong khoảng thời gian đó.
\(\overrightarrow {{p_2}} - \overrightarrow {{p_1}} = \Delta \overrightarrow p = \overrightarrow F \Delta t\)
Ta có: Do vật chuyển động không vận tốc đầu nên:
\(\begin{array}{l}\Delta \overrightarrow p = \overrightarrow {{p_2}} = \overrightarrow p = \overrightarrow F t\\ \to \overrightarrow p = \overrightarrow F t\end{array}\)
Câu hỏi 5 :
Trong quá trình dao động của một con lắc đơn thì tại vị trí cân bằng
- A
động năng đạt giá trị cực đại
- B
thế năng đạt giá trị cực đại
- C
cơ năng bằng không
- D
thế năng bằng động năng
Đáp án: A
Phương pháp giải:
Vận dụng định luật bảo toàn cơ năng và các biểu thức tính động năng, thế năng
+ Biểu thức tính động năng: \({{\rm{W}}_d} = \dfrac{1}{2}m{v^2}\)
+ Biểu thức tính thế năng: \({{\rm{W}}_t} = mgz\)
Lời giải chi tiết:
A – đúng
B – sai vì: Tại VTCB thế năng của con lắc cực tiểu
C – sai vì: Cơ năng của con lắc được bảo toàn
D – sai vì: Tại VTCB động năng cực đại, thế năng cực tiểu và cơ năng bảo toàn
Câu hỏi 6 :
Đặc điểm nào sau đây không phải của quá trình đẳng áp đối với một khối khí lý tưởng xác định:
- A
Khi thể tích giảm thì nhiệt độ giảm
- B
Áp suất của chất khí không đổi
- C
Khi áp suất tăng thì thể tích giảm
- D
Khi nhiệt độ tăng thì thể tích tăng
Đáp án: C
Phương pháp giải:
Vận dụng định luật Gay Luy-xác
Lời giải chi tiết:
Đặc điểm không phải của quá trình đẳng áp đối với một khối khí lý tưởng xác định là:Khi áp suất tăng thì thể tích giảm
Câu hỏi 7 :
Vật nào sau đây không có khả năng sinh công?
- A
Dòng nước lũ đang chảy mạnh.
- B
Viên đạn đang bay.
- C
Búa máy đang rơi.
- D
Hòn đá đang nằm trên mặt đất.
Đáp án: D
Lời giải chi tiết:
Hòn đá nằm trên mặt đất không có khả năng sinh công.
Câu hỏi 8 :
Biểu thức nào sau đây xác định thế năng hấp dẫn của một vật có khối lượng m, ở độ cao h so với mặt đất. Chọn gốc thế năng ở mặt đất
- A
\({{\rm{W}}_t} = \frac{{mg}}{h}\)
- B
\({{\rm{W}}_t} = mgh\)
- C
\({{\rm{W}}_t} = kgh\)
- D
\({{\rm{W}}_t} = \frac{{hg}}{m}\)
Đáp án: B
Phương pháp giải:
Sử dụng biểu thức xác định thế năng đàn hồi
Lời giải chi tiết:
Nếu chọn gốc thế năng là mặt đất thì công thức tính thế năng trọng trường của một vật ở độ cao h là:
\({{\rm{W}}_t} = mgh\)
Câu hỏi 9 :
Thế năng đàn hồi của một lò xo không phụ thuộc vào:
- A
Độ cứng của lò xo
- B
Độ biến dạng của lò xo
- C
Mốc thế năng
- D
Chiều biến dạng của lò xo
Đáp án: D
Phương pháp giải:
Vận dụng biểu thức tính thế năng đàn hồi: \({{\rm{W}}_t} = \dfrac{1}{2}k{\left( {\Delta l} \right)^2}\)
Lời giải chi tiết:
Ta có, thế năng đàn hồi \({{\rm{W}}_t} = \dfrac{1}{2}k{\left( {\Delta l} \right)^2}\)
=> Thế năng đàn hồi không phụ thuộc vào chiều biến dạng của lò xo
Câu hỏi 10 :
Phát biểu nào sau đây là không đúng khi nói về quá trình đẳng nhiệt của một lượng khí xác định?
- A
Áp suất tỉ lệ nghịch với thể tích.
- B
Tích của áp suất và thể tích là một hằng số.
- C
Trên giản đồ p – V, đồ thị là một đường hypebol.
- D
Áp suất tỉ lệ thuận với thể tích.
Đáp án: D
Lời giải chi tiết:
Ta có: Định luật Bôilơ - Mariốt:
Trong quá trình đẳng nhiệt của một lượng khí nhất định, áp suất tỉ lệ nghịch với thể tích.
\(p \sim \frac{1}{V} \to pV = h/s\)
=> Các phương án:
A, B, C - đúng
D - sai
Câu hỏi 11 :
Phát biểu nào sau đây đúng khi nói về định luật Gay Luy-xác
- A
Trong quá trình đẳng áp của một lượng khí nhất định, thể tích tỉ lệ nghịch với nhiệt độ tuyệt đối.
- B
Trong quá trình đẳng áp của một lượng khí nhất định, thể tích tỉ lệ thuận với áp suất
- C
Trong quá trình đẳng áp của một lượng khí nhất định, thể tích tỉ lệ nghịch với nhiệt độ Celsius
- D
Trong quá trình đẳng áp của một lượng khí nhất định, thể tích tỉ lệ thuận với nhiệt độ tuyệt đối.
Đáp án: D
Phương pháp giải:
Sử dụng định nghĩa về định luật Gay Luy-xác
Lời giải chi tiết:
Định luật Gay Luy - xác:
Trong quá trình đẳng áp của một lượng khí nhất định, thể tích tỉ lệ thuận với nhiệt độ tuyệt đối.
Câu hỏi 12 :
Chon phương án sai khi nói về các tính chất của chất khí
- A
Bành trướng là chiếm một phần thể tích của bình chứa
- B
Khi áp suất tác dụng lên một lượng khí tăng thì thể tích của khí giảm đáng kể.
- C
Chất khí có tính dễ nén
- D
Chất khí có khối lượng riêng nhỏ so với chất rắn và chất lỏng
Đáp án: A
Lời giải chi tiết:
A - sai vì: Bành trướng: Chiếm toàn bộ thể tích của bình chứa
B, C, D - đúng
Câu hỏi 13 :
Công thức không mô tả phương trình trạng thái của khí lí tưởng là:
- A
\(\frac{{pV}}{T} = const\)
- B
\(\frac{{{p_1}{V_1}}}{{{T_1}}} = \frac{{{p_2}{V_2}}}{{{T_2}}}\)
- C
\(pV \sim T\)
- D
\(\frac{{pT}}{V} = const\)
Đáp án: D
Phương pháp giải:
Sử dụng biểu thức phương trình trạng thái của khí lý tưởng
Lời giải chi tiết:
Phương trình trạng thái của khí lý tưởng: \(\frac{{pV}}{T} = const\)
Câu hỏi 14 :
Động năng là đại lượng:
- A
Vô hướng, luôn dương hoặc bằng không.
- B
Vô hướng, có thể âm, dương hoặc bằng không.
- C
Véctơ, luôn dương.
- D
Véctơ, luôn dương hoặc bằng không.
Đáp án: A
Phương pháp giải:
Vận dụng biểu thức tính động năng: \({{\rm{W}}_d} = \dfrac{1}{2}m{v^2}\)
Lời giải chi tiết:
Ta có biểu thức tính động năng: \({{\rm{W}}_d} = \dfrac{1}{2}m{v^2}\)
=> Động năng là đại lượng vô hướng, luôn dương hoặc bằng không
Câu hỏi 15 :
Động năng được tính bằng biểu thức:
- A
\({W_d} = \dfrac{1}{2}{m^2}{v^2}\)
- B
\({W_d} = \dfrac{1}{2}{m^2}v\)
- C
\({W_d} = \dfrac{1}{2}m{v^2}\)
- D
\({W_d} = \dfrac{1}{2}mv\)
Đáp án: C
Lời giải chi tiết:
Biểu thức tính động năng : \({{\rm{W}}_d} = \dfrac{1}{2}m{v^2}\)
Câu hỏi 16 :
Một tên lửa vũ trụ khi bắt đầu rời bệ phóng trong giây đầu tiên đã phụt ra một lượng khí đốt 1300 kg với vận tốc 2500m/s. Lực đẩy tên lửa tại thời điểm đó là :
- A 3,5.106 N.
- B 3,25.106 N
- C 3,15.106 N
- D 32,5.106 N
Đáp án: B
Phương pháp giải:
Động lượng \(\overrightarrow p \)của một vật là một vecto cùng hướng với vận tốc của vật và được xác định bởi công thức: \(\overrightarrow p = m.\overrightarrow v \)
Độ biến thiên động lượng: \(\overrightarrow {\Delta p} = \overrightarrow {{p_2}} - \overrightarrow {{p_1}} \)
+ Xung của lực: \(\overrightarrow F = \dfrac{{\overrightarrow p }}{{\Delta t}}\)
Lời giải chi tiết:
Độ biến thiên động lượng của khí phụt ra trong giây đầu tiên:
\(\Delta p = mv = 1300.2500 = 3\,250\,000kg.m/s\)
Lực đẩy của tên lửa tại thời điểm đó:
\(F = \dfrac{{\Delta p}}{{\Delta t}} = \dfrac{{3\,250\,000}}{1} = 3,{25.10^6}N\)
Câu hỏi 17 :
Kéo một xe goòng bằng một sợi dây cáp với một lực bằng 250N. Góc giữa dây cáp và mặt phẳng nằm ngang bằng 450. Công của lực tác dụng lên xe để xe chạy được 300m có giá trị là:
- A 50000 J
- B 35000 J
- C 25980 J
- D 53033 J
Đáp án: D
Phương pháp giải:
Công thức tính công: \(A = F.s.\cos \alpha ;\,\,\alpha = \left( {\overrightarrow F ;\overrightarrow s } \right)\)
Lời giải chi tiết:
Công của lực tác dụng lên xe:
\(A = F.s.\cos \alpha = 250.300.\cos 45 = 53033J\)
Câu hỏi 18 :
Một ô tô tải (xe 1) khối lượng 6 tấn và một ô tô con (xe 2) khối lượng 1200kg chuyển động cùng chiều trên đường, chiếc trước chiếc sau với cùng vận tốc không đổi 72km/h. Động năng của mỗi ô tô là:
- A \({{\rm{W}}_{d1}} = 1\,200\,000J;{{\rm{W}}_{d2}} = 240\,000J\)
- B \({{\rm{W}}_{d1}} = 240\,000;{{\rm{W}}_{d2}} = 1\,200\,000JJ\)
- C \({{\rm{W}}_{d1}} = 1\,600\,000J;{{\rm{W}}_{d2}} = 2500\,000J\)
- D \({{\rm{W}}_{d1}} = 2500\,000;{{\rm{W}}_{d2}} = 1\,600\,000JJ\)
Đáp án: A
Phương pháp giải:
Động năng là dạng năng lượng của một vật có được do nó đang chuyển động và được xác định theo công thức: \({{\rm{W}}_d} = \dfrac{1}{2}m{v^2}\)
Lời giải chi tiết:
Ta có: \(\left\{ \begin{array}{l}{m_1} = 6T = 6000kg\\{m_2} = 1200kg\\{v_1} = {v_2} = 72km/h = 20m/s\end{array} \right.\)
Động năng của mỗi ô tô là:
\(\left\{ \begin{array}{l}{{\rm{W}}_{d1}} = \dfrac{1}{2}mv_1^2 = \dfrac{1}{2}{.6000.20^2} = 1\,200\,000J\\{{\rm{W}}_{d2}} = \dfrac{1}{2}mv_2^2 = \dfrac{1}{2}{.1200.20^2} = 240\,000J\end{array} \right.\)
Câu hỏi 19 :
Dưới tác dụng của lực bằng \(5N\) lò xo bị giãn ra \(2 cm\). Công của ngoại lực tác dụng để lò xo giãn ra \(5 cm\) là:
- A
0,31 J.
- B
0,25 J.
- C
15 J.
- D
25 J.
Đáp án: A
Phương pháp giải:
Vận dụng biểu định luật Húc và công
+ Biểu thức định luật Húc: \(F=|kx|\)
+ Công: \(A=W_t=\dfrac{kx^2}{2}\)
Lời giải chi tiết:
Theo định luật Húc: \({F_{dh}} = k.\left( {\Delta l} \right) \Rightarrow k = \dfrac{F}{{\Delta l}} = \dfrac{5}{{0,02}} = 250N/m\).
Công của ngoại lực tác dụng để lò xo giãn ra \(5 cm\) là: \(A = {W_t} = \dfrac{1}{2}k{x^2} = \dfrac{1}{2}.250.{\left( {0,05} \right)^2} = 0,3125J\)\( \approx 0,31J\).
Câu hỏi 20 :
Một hòn bi có khối lượng 50g được ném thẳng đứng lên cao với vận tốc 6m/s từ độ cao 1,2m so với mặt đất. Chọn gốc thế năng tại mặt đất, lấy g = 10m/s2. Độ cao cực đại mà bi đạt được
- A 2,75m
- B 2,25m
- C 2,5m
- D 3m
Đáp án: D
Phương pháp giải:
Cơ năng của vật chuyển động trong trọng trường: \({\rm{W}} = {{\rm{W}}_d} + {{\rm{W}}_t} = \dfrac{1}{2}m{v^2} + mgz\)
Khi một vật chuyển động trong trọng trường chỉ chịu tác dụng của trọng lực thì cơ năng của vật là một đại lượng bảo toàn.
Lời giải chi tiết:
+ Tại vị trí ném ta có : \(\left\{ \begin{array}{l}{v_1} = 6m/s\\{z_1} = 1,2m\end{array} \right.\)
Cơ năng của vật : \({{\rm{W}}_1} = \dfrac{1}{2}mv_1^2 + mg{z_1} = \dfrac{1}{2}.0,{05.6^2} + 0,05.10.1,2 = 1,5J\)
+ Tại vị trí vật có độ cao cực đại : \(\left\{ \begin{array}{l}{v_2} = 0\\{z_2} = {h_{\max }}\end{array} \right.\)
Cơ năng của vật : \({{\rm{W}}_2} = mg{z_2} = 0,05.10.{h_{\max }} = 0,5.{h_{\max }}\,\,\left( J \right)\)
+ Cơ năng của vật được bảo toàn nên :
\({{\rm{W}}_1}{\rm{ = }}{{\rm{W}}_2} \Leftrightarrow 0,5.{h_{\max }} = 1,5 \Rightarrow {h_{\max }} = 3m\)
Câu hỏi 21 :
Một người đi xe đạp có khối lượng tổng cộng của cả xe và người là 45kg đang chuyển động đều với vận tốc 18km/h thì nhìn thấy một vũng nước sâu cách 8m. Để không rơi vào vũng nước thì người đó phải dùng một lực hãm có độ lớn tối thiểu là:
- A
\(70,3N\)
- B
\(113,9N\)
- C
\(1822,5N\)
- D
\(140,6N\)
Đáp án: A
Phương pháp giải:
Sử dụng định lí biến thiên động năng: \({{\rm{W}}_{{d_2}}} - {{\rm{W}}_{{d_1}}} = A\)
Lời giải chi tiết:
Từ định lí biến thiên động năng ta có:
\(\begin{array}{l}A = {W_{d2}} - {W_{d1}}\\ \Leftrightarrow {F_h}.s = 0 - \dfrac{1}{2}m{v^2}\\ \Rightarrow F{}_h = - \dfrac{{m{v^2}}}{{2s}}\end{array}\)
Ta có : \(\left\{ \begin{array}{l}v = 18km/h = 5m/s\\m = 45kg\\s = 8m\end{array} \right.\)
\( \Rightarrow {F_h} = - \dfrac{{{{45.5}^2}}}{{2.8}} \approx - 70,3N\)
Độ lớn của lực hãm là: \( \Rightarrow {F_h} = 70,3N\)dấu ‘-‘ có nghĩa là lực cản trở chuyển động.
Câu hỏi 22 :
Hai viên bi có khối lượng m1 = 3kg và m2 = 2kg chuyển động trên mặt phẳng ngang ngược chiều nhau với các vận tốc tương ứng v1 = 1m/s, v2 = 2m/s. Coi va chạm của hai viên bi là hoàn toàn đàn hồi xuyên tâm. Chọn chiều dương là chiều chuyển động ban đầu của viên bi 1. Vận tốc ngay sau va chạm của viên bi 1 và viên bi 2 lần lượt là:
- A
v1’ = 1,8 m/s và v2’ = –1,4 m/s
- B
v1’ = -1,4 m/s và v2’ = 1,6 m/s
- C
v1’ = 1,8 m/s và v2’ = 1,6 m/s
- D
v1’ = – 1,4 m/s và v2’ = – 1,6 m/s
Đáp án: B
Phương pháp giải:
Vận dụng lý thuyết va chạm đàn hồi trực diện
\({v_1}' = \frac{{\left( {{m_1} - {m_2}} \right){v_1} + 2{m_2}{v_2}}}{{{m_1} + {m_2}}}\)
\({v_2}' = \frac{{\left( {{m_2} - {m_1}} \right){v_2} + 2{m_1}{v_1}}}{{{m_1} + {m_2}}}\)
\({v_1},{v_2},{v_1}',{v_2}'\) là các giá trị đại số có thể âm, dương hoặc bằng 0 tùy vào từng trường hợp cụ thể và hệ quy chiếu ta chọn
Lời giải chi tiết:
Hai vật va chạm đàn hồi trực diện. Chọn chiều dương là chiều chuyển động của viên bi 1 nên vận tốc của viên bi 2 là: \({v_2} = - 2m/s\) . Ta có:
\({v_1}' = \frac{{\left( {{m_1} - {m_2}} \right){v_1} + 2{m_2}{v_2}}}{{{m_1} + {m_2}}} = \frac{{\left( {3 - 2} \right).1 - 2.2.2}}{{3 + 2}} = - 1,4m/s\)
\({v_2}' = \frac{{\left( {{m_2} - {m_1}} \right){v_2} + 2{m_1}{v_1}}}{{{m_1} + {m_2}}} = \frac{{\left( {2 - 3} \right).( - 2) + 2.3.1}}{{3 + 2}} = 1,6\,m/s\)
Câu hỏi 23 :
Một quả bóng da có dung tích \(2,5\) lít. Người ta bơm không khí ở áp suất \({10^5}Pa\) vào bóng. Mỗi lần bơm được \(125c{m^3}\) không khí. Biết trước khi bơm, trong bóng có không khí ở áp suất \({10^5}Pa\) và nhiệt độ không đổi trong thời gian bơm. Áp suất không khí trong quả bóng sau \(20\) lần bơm bằng: (coi quả bóng trước khi bơm không có không khí).
- A
\({5.10^5}Pa\)
- B
\(2,{5.10^5}Pa\)
- C
\({2.10^5}Pa\)
- D
\(7,{5.10^5}Pa\)
Đáp án: C
Phương pháp giải:
Vận dụng định luật Bôilơ - Mariốt: \(pV = h/s\)
Lời giải chi tiết:
Ta có:
Thể tích khí bơm được sau 20 lần bơm là \(20.0,125\) lít
+ Thể tích của không khí trước khi bơm vào bóng: \({V_1} = 20.0,125 + 2,5 = 5l\) (Bao gồm thể tích khí của 20 lần bơm và thể tích khí của khí có sẵn trong bóng)
+ Sau khi bơm khí vào trong bóng thể tích lượng khí chính bằng thể tích của bóng: \({V_2} = 2,5l\)
Do nhiệt đọ không đổi, theo định luật Bôi lơ – Ma ri ốt, ta có:
\(\begin{array}{l}{p_1}{V_1} = {p_2}{V_2}\\ \Leftrightarrow {10^5}.5 = {p_2}.2,5\\ \Rightarrow {p_2} = {2.10^5}Pa\end{array}\)
Câu hỏi 24 :
Một bình được nạp khí ở nhiệt độ 350C dưới áp suất 350kPa. Sau đó bình được chuyển đến một nơi có nhiệt độ 400C, tính độ tăng áp suất của khí trong bình.
- A 2kPa
- B 4kPa
- C 6kPa
- D 8kPa
Đáp án: C
Phương pháp giải:
Định luật Sác - lơ: Trong quá trình đẳng tích của một lượng khí nhất định, áp suất tỉ lệ thuận với nhiệt độ tuyệt đối.
Hệ thức: \(p \sim T \Rightarrow \dfrac{p}{T} = const\)
Lời giải chi tiết:
Áp dụng định luật Sác – lơ ta có:
\(\dfrac{{{p_1}}}{{{T_1}}} = \dfrac{{{p_2}}}{{{T_2}}} \Rightarrow {p_2} = \dfrac{{{p_1}{T_2}}}{{{T_1}}} = \dfrac{{350.313}}{{308}} \approx 356kPa\)
Độ tăng áp suất của khí trong bình là:\(\Delta p = 356 - 350 = 6kPa\)
Câu hỏi 25 :
Một khối khí lí tưởng thực hiện quá trình như hình vẽ.
- A
\(1,58atm\)
- B
\(10,13atm\)
- C
\(9,87atm\)
- D
\({10.10^5}atm\)
Đáp án: A
Phương pháp giải:
+ Áp dụng biểu thức tính nhiệt độ tuyệt đối: \(T = t + 273\)
+ Vận dụng biểu thức định luật Sáclơ: \(\dfrac{p}{T} = const\)
Lời giải chi tiết:
Ta có:
Lượng không khí trong bình được đun nóng trong một quá trình đẳng tích.
Trạng thái 1: \(\left\{ \begin{array}{l}{t_1}\; = {\rm{ 120}}K\\{p_1}\; = {\rm{ ?}}\end{array} \right.\) .
Trạng thái 2: \(\left\{ \begin{array}{l}{t_1}\; = 300K\\{p_2}\; = 4atm\end{array} \right.\)
Trong quá trình đẳng tích:
\(\dfrac{{{p_2}}}{{{T_2}}} = \dfrac{{{p_1}}}{{{T_1}}} \to {p_1} = \dfrac{{{p_2}{T_1}}}{{{T_1}}} = 1,58atm\)
Câu hỏi 26 :
Cho áp kế như hình vẽ.
- A
\(106,2c{m^3}\)
- B
\(106,5c{m^3}\)
- C
\(130c{m^3}\)
- D
\(250c{m^3}\)
Đáp án: A
Phương pháp giải:
+ Vận dụng biểu thức tính nhiệt độ tuyệt đối: \(T = t + 273\)
+ Vận dụng biểu thức tính thể tích: \(V = l{\rm{S}}\)
+ Vận dụng biểu thức định luật Gay Luy - xác: \(\dfrac{V}{T} = h/{\rm{s}}\)
Lời giải chi tiết:
Ta có:
- Trạng thái 1: \(\left\{ \begin{array}{l}{T_1} = 273K\\{V_1} = V + {l_1}S = V + 30.0,1(c{m^3})\end{array} \right.\)
- Trạng thái 2: \(\left\{ \begin{array}{l}{T_2} = 5 + 273 = 278K\\{V_2} = V + {l_2}S = V + 50.0,1(c{m^3})\end{array} \right.\)
Áp dụng định luật Gay Luy-xác, ta có:
\(\begin{array}{l}\dfrac{{{V_1}}}{{{T_1}}} = \dfrac{{{V_2}}}{{{T_2}}} \leftrightarrow \dfrac{{V + 3}}{{273}} = \dfrac{{V + 5}}{{278}}\\ \to V = 106,2c{m^3}\end{array}\)
Câu hỏi 27 :
Khí cầu có dung tích \(328{m^3}\) được bơm khí Hiđro. Khi bơm xong, hiđro trong khí cầu có nhiệt độ \({27^0}C\), áp suất \(0,9atm\). Hỏi phải bơm bao nhiêu lâu nếu mỗi giây bơm được \(2,5g\) hiđro vào khí cầu.
- A
\(\dfrac{1}{3}h\)
- B
\(\dfrac{2}{3}h\)
- C
\(\dfrac{4}{3}h\)
- D
\(\dfrac{8}{3}h\)
Đáp án: D
Phương pháp giải:
+ Vận dụng biểu thức tính nhiệt độ tuyệt đối: \(T = t + 273\)
+ Vận dụng phương trình Cla-pe-rôn - Men-đê-lê-ép: \(pV = n{\rm{R}}T = \dfrac{m}{M}RT\)
(c2)
Lời giải chi tiết:
Ta có:
- Thể tích: \(V = 328{m^3} = {328.10^3}l\)
- Nhiệt độ: \(T = 27 + 273 = 300K\)
- Áp suất: \(p = 0,0{\rm{a}}tm\)
Gọi m là khối khí đã bơm vào khí cầu, áp dụng phương trình Cla-pe-rôn - Men-đê-lê-ép, ta có:
\(pV = \dfrac{m}{M}RT \to m = M\dfrac{{pV}}{{RT}} = 2.\dfrac{{0,{{9.328.10}^3}}}{{0,082.300}} = 24000g\)
Biết mỗi giây bơm được \(2,5g\) hiđrô vào khí cầu
=> Thời gian để bơm được \(m\left( g \right)\) hiđrô vào khí cầu là:
\(t = \dfrac{m}{{2,5}} = \dfrac{{24000}}{{2,5}} = 9600{\rm{s}} = 160phut= \dfrac{8}{3}h\)
Câu hỏi 28 :
Một bình có thể tích \(5,6l\), chứa \(64g\) khí oxi ở nhiệt độ \({0^0}C\). Áp suất của khí trong bình là:
- A
\(1atm\)
- B
\(2atm\)
- C
\(4atm\)
- D
\(8atm\)
Đáp án: D
Phương pháp giải:
+ Sử dụng phương trình Cla – pê – rôn – Men – đê – lê – ép: \(p.V = n.R.T = \dfrac{m}{M}.R.T\)
Trong đó:
+ p: áp suất chất khí (Pa)
+ V: thể tích chất khí (m3)
+ R: hằng số của các khí (R = 8,31 J/mol.K)
+ m: khối lượng chất (g)
+ M: khối lượng mol phân tử chất khí (g/mol)
+ T: nhiệt độ tuyệt đối (K)
+ Đổi đơn vị áp suất: \(1atm = {1,013.10^5}Pa\)
Lời giải chi tiết:
- Ta có: \(V = 5,6l = {5,6.10^{ - 3}}{m^3}\) ; \(m = 64{\rm{ }}g\); \(T = 0 + 273 = 273K\)
- Áp dụng phương trình Cla – pê – rôn – Men – đê – lê – ép, ta có: \(p.V = n.R.T = \dfrac{m}{M}.R.T\)
\( \to p = \dfrac{m}{M}.\dfrac{{RT}}{V} = \dfrac{{64}}{{32}}.\dfrac{{8,31.273}}{{{{5,6.10}^{ - 3}}}} = 810225\left( {Pa} \right)\)
Lại có: \(1atm = {1,013.10^5}Pa\)
\( \to p = \dfrac{{810225}}{{{{1,013.10}^5}}} \approx 8atm\)
Câu hỏi 29 :
Một khối khí lí tưởng thực hiện quá trình được biểu diễn như hình.
- A
\({149^0}C\)
- B
\(149K\)
- C
\(374K\)
- D
\({77^0}C\)
Đáp án: B
Phương pháp giải:
Áp dụng phương trình trạng thái của khí lí tưởng: \(\dfrac{{pV}}{T} = hs\)
Lời giải chi tiết:
Xét các trạng thái của khí:
+ Trạng thái 1: \(\left\{ \begin{array}{l}{p_1} = 3,1\\{V_1} = 7\\{T_1} = 37 + 273 = 310K\end{array} \right.\)
+ Trạng thái 2: \(\left\{ \begin{array}{l}{p_2} = 5,2\\{V_2} = 2\\{T_2} = ?\end{array} \right.\)
Áp dụng phương trình trạng thái của khí lí tưởng, ta có: \(\dfrac{{{p_1}{V_1}}}{{{T_1}}} = \dfrac{{{p_2}{V_2}}}{{{T_2}}}\)
\( \Rightarrow {T_2} = \dfrac{{{p_2}{V_2}}}{{{p_1}{V_1}}}{T_1} = \dfrac{{5,2.2}}{{3,1.7}}.310 = 148,6K\)
Câu hỏi 30 :
Vật đang chuyển động với vận tốc 15 m/s thì trượt lên dốc. Biết dốc dài 50m, cao 25m, hệ số ma sát giữa vật và dốc là 0,2. Lấy g = 10m/s2. Quãng đường vật đi được đến khi dừng lại là bao nhiêu? Vật có lên hết dốc không?
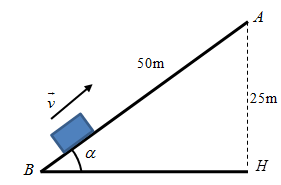
- A 28,71; Vật không lên được hết dốc
- B 16,71m; Vật không lên được hết dốc
- C 50m; Vật lên được hết dốc
- D 60,1m; Vật lên được hết dốc
Đáp án: B
Phương pháp giải:
Công thức tính công : \(A = F.s.\cos \alpha ;\,\,\alpha = \left( {\overrightarrow s ;\overrightarrow F } \right)\)
Cơ năng của vật chuyển động trong trọng trường : \({\rm{W}} = \dfrac{1}{2}.m.{v^2} + m.g.z\)
Công của lực ma sát bằng độ biến thiên cơ năng.
Lời giải chi tiết:
Vì có ma sát nên cơ năng không bảo toàn. Chọn mốc thế năng tại chân dốc
Gọi C là vị trí có vận tốc bằng 0.
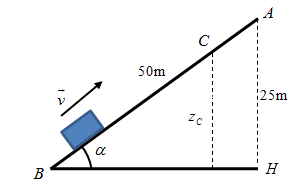
+ Tại B có:
\(\left\{ \begin{array}{l}{v_B} = 15m/s\\{z_B} = 0\end{array} \right.\) \( \Rightarrow {{\rm{W}}_B} = {{\rm{W}}_{dB}} + {{\rm{W}}_{tB}} = \dfrac{1}{2}mv_B^2 = 112,5.m\,\,\left( J \right)\)
+ Tại C có:
\(\begin{array}{l}\left\{ \begin{array}{l}{v_C} = 0\\{z_C} = BC.\sin \alpha = BC.\dfrac{{25}}{{50}} = 0,5.BC\,\,\,\left( m \right)\end{array} \right.\\ \Rightarrow {{\rm{W}}_C} = {{\rm{W}}_{tC}} = mg{z_C} = m.10.0,5.BC = 5.BC.m\,\,\left( J \right)\end{array}\)
Độ lớn lực ma sát :
\({F_{ms}} = \mu mg.\cos \alpha = \mu mg.\sqrt {1 - 0,{5^2}} = 0,2.m.10.\dfrac{{\sqrt 3 }}{2} = \sqrt 3 \,.m\,\left( N \right)\)
Do công của lực ma sát bằng độ biến thiên của cơ năng nên:
\(\begin{array}{l}{{\rm{W}}_C} - {{\rm{W}}_B} = {A_{\overrightarrow {{F_{ms}}} }} \Leftrightarrow 5.BC.m - 112,5.m = \sqrt 3 .m.BC.\cos 180\\ \Leftrightarrow 5.BC - 112,5 = - \sqrt 3 .BC \Rightarrow BC = 16,71m\end{array}\)
Vì BC < AB → Vật không lên được hết dốc
