Đề bài
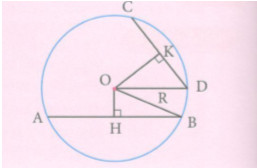
Cho đường tròn (O ; 10 cm) và hai dây AB = 8 cm, CD = 6 cm. Từ O hạ OH và OK theo thứ tự vuông góc với AB và CD.
Hãy tính OH, OK và cho biết đoạn nào dài hơn.
Lời giải chi tiết
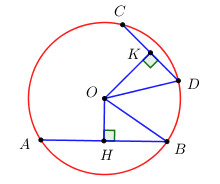
Ta có \(OH \bot AB,\,\,OK \bot CD \Rightarrow \) H, K theo thứ tự là trung điểm của \(AB,\,\,CD\).
\( \Rightarrow HB = \dfrac{1}{2}AB = \dfrac{1}{2}.8 = 4\,\,\left( {cm} \right),\)\(\,\,KD = \dfrac{1}{2}CD = \dfrac{1}{2}.6 = 3\,\,\left( {cm} \right)\)
Áp dụng định lí Pytago trong tam giác vuông \(OHB\) có:
\(O{H^2} = O{B^2} - H{B^2} = {10^2} - {4^2} = 84 \)
\(\Leftrightarrow OH = \sqrt {84} = 2\sqrt {21} \,\,\left( {cm} \right)\)
Áp dụng định lí Pytago trong tam giác vuông \(OKD\) có:
\(O{K^2} = O{D^2} - K{D^2} = {10^2} - {3^2} = 91\)
\(\Leftrightarrow OK = \sqrt {91} \,\,\left( {cm} \right)\)
Do \(91 > 84 \Rightarrow \sqrt {91} > \sqrt {84} \Rightarrow OK > OH\).
Vậy \(OK > OH\).
soanvan.me
