ĐẠI CƯƠNG VỀ DÒNG ĐIỆN XOAY CHIỀU
Cho khung dây dẫn có diện tích S gồm có N vòng dây quay đều với vận tốc góc ω xung quanh trục đối xứng x’x trong từ trường đều có \(\vec B \bot \) xx '.
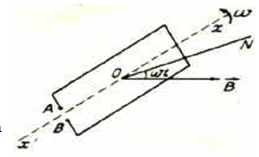
1. TỪ THÔNG GỬI QUA KHUNG DÂY
Từ thông gởi qua khung là \(\Phi = NBScos(\omega t + \varphi ){\rm{ }}Wb\) .
Đặt \({\Phi _0} = NB{\rm{S}} \to \Phi = {\Phi _0}\cos (\omega t + \varphi )\)
\({\Phi _0}\) được gọi là từ thông cực đại
2. SUẤT ĐIỆN ĐỘNG XOAY CHIỀU
Theo hiện tượng cảm ứng điện từ trong khung hình thành suất điện động cảm ứng có biểu thức:
\(e{\rm{ }} = -\Phi ' = \omega NBSsin(\omega t + \varphi ).\)
Đặt \({E_0} = \omega NBS = \omega {\Phi _0} \to e = {E_0}sin(\omega t + \varphi ) = {E_0}cos(\omega t + \varphi - \dfrac{\pi }{2})\)
Vậy suất điện động trong khung dây biến thiên tuần hoàn với tần số góc ω và chậm pha hơn từ thông góc π/2. Nếu mạch ngoài kín thì trong mạch sẽ có dòng điện, điện áp gây ra ở mạch ngoài cũng biến thiên điều hòa: u = U0cos(ωt + φu) V.
Đơn vị : S (m2), Φ (Wb) – Webe, B (T) – Testla, N (vòng), ω (rad/s), e (V)…
\(1{\rm{ }}vong/phut = \dfrac{{2\pi }}{{60}} = (rad/s{\rm{ }});{\rm{ }}1{\rm{ }}c{m^2} = {10^{ - 4}}{m^2}\)
3. KHÁI NIỆM VỀ DÒNG ĐIỆN XOAY CHIỀU
- Định nghĩa:
Dòng điện xoay chiều là dòng điện có cường độ dòng điện biến đổi điều hòa theo thời gian (theo hàm cosin hay sin) => Dòng điện xoay chiều thay đổi cả về cường độ và phương chiều.
- Biểu thức: \(i = {I_0}\cos (\omega t + {\phi _i})A\)
Trong đó:
\(i:\) giá trị cường độ dòng điện xoay chiều tức thời, đơn vị là (A)
\({I_0} > {\rm{ }}0\) : giá trị cường độ dòng điện cực đại của dòng điện xoay chiều
\(\omega ,{\varphi _i}:\) là các hằng số.
\(\omega > {\rm{ }}0\) là tần số góc.
\((\omega t{\rm{ }} + {\varphi _i}):\) pha tại thời điểm t.
\(\varphi i{\rm{ }}:\) Pha ban đầu của dòng điện.
- Chu kỳ, tần số của dòng điện :\(\left\{ \begin{array}{l}T = \dfrac{{2\pi }}{\omega } = \dfrac{1}{f}(s)\\f = \dfrac{1}{T} = \dfrac{\omega }{{2\pi }}(Hz)\end{array} \right.\)
4. ĐỘ LỆCH PHA CỦA ĐIỆN ÁP VÀ DÒNG ĐIỆN
Đặt \(\varphi = {\varphi _u}-{\varphi _i},\) được gọi là độ lệch pha của điện áp và dòng điện trong mạch.
+ Nếu \(\varphi > {\rm{ }}0\) thì khi đó điện áp nhanh pha hơn dòng điện hay dòng điện chậm pha hơn điện áp.
+ Nếu \(\varphi < {\rm{ }}0\) thì khi đó điện áp chậm pha hơn dòng điện hay dòng điện nhanh pha hơn điện áp.
- Khi độ lệch pha của điện áp và dòng điện là π/2 thì ta có phương trình của dòng điện và điện áp thỏa mãn \(\left\{ \begin{array}{l}u = {U_0}\cos (\omega t)\\i = {I_0}\cos (\omega t \pm \dfrac{\pi }{2}) = \mp {I_0}\sin (\omega t)\end{array} \right. \to {\left( {\dfrac{u}{{{U_0}}}} \right)^2} + {\left( {\dfrac{i}{{{I_0}}}} \right)^2} = 1\)
- Nếu điện áp vuông pha với dòng điện, đồng thời tại hai thời điểm t1, t2 điện áp và dòng điện có các cặp giá trị tương ứng là u1; i1 và u2; i2 thì ta có: \({\left( {\dfrac{{{u_1}}}{{{U_0}}}} \right)^2} + {\left( {\dfrac{{{i_1}}}{{{I_0}}}} \right)^2} = {\left( {\dfrac{{{u_2}}}{{{U_0}}}} \right)^2} + {\left( {\dfrac{{{i_2}}}{{{I_0}}}} \right)^2} \to \dfrac{{{U_0}}}{{{I_0}}} = \sqrt {\dfrac{{u_1^2 - u_2^2}}{{i_1^2 - i_2^2}}} \)
5. GIÁ TRỊ HIỆU DỤNG.
Ngoài ra, đối với dòng điện xoay chiều, các đại lượng như điện áp, suất điện động, cường độ dòng điện , … cũng là hàm số sin hay cosin của thời gian.
Các đại lượng có giá trị hiệu dụng: \(I{\rm{ }} = \dfrac{{{I_0}}}{{\sqrt 2 }}\), \(U{\rm{ }} = \dfrac{{{U_0}}}{{\sqrt 2 }}\), \(E{\rm{ }} = \dfrac{{{E_0}}}{{\sqrt 2 }}\)
Nhiệt lượng tỏa ra trên điện trở R trong thời gian t nếu có dòng điện xoay chiều i=I0cos(ωt+φ) chạy qua là: \(Q = P.t = \dfrac{{I_0^2}}{2}Rt\)
Công suất tỏa nhiệt trên R khi có dòng điện xoay chiều chạy qua: \(P = {I^2}R\)
Sơ đồ tư duy về đại cương dòng điện xoay chiều

