Dạng 1: Xác định từ thông qua khung dây và suất điện động xoay chiều
Sử dụng các công thức:
- Từ thông:
\(\Phi = NB{\rm{S}}\cos \left( {\omega t + \varphi } \right) = {\Phi _0}\cos \left( {\omega t + \varphi } \right)\) (Wb)
Trong đó:
+ N: số vòng dây
+ S: tiết diện vòng dây (m2)
+ B: cảm ứng từ (T)
+ \({\Phi _0} = NB{\rm{S}}\): từ thông cực đại qua khung dây (Wb)
+ \(\omega \): tốc độ quay của khung dây (rad/s)
- Suất điện động xoay chiều:
\(e = - \Phi ' = {E_0}\cos \left( {\omega t + \varphi } \right)\) (V)
Trong đó: \({E_0} = NB{\rm{S}}\omega = \omega {\Phi _0}\): suất điện động xoay chiều cực đại (V)
*Chú ý: Khi trong khung dây có suất điện động thì hai đầu khung dây có điện áp (hiệu điện thế). Nếu khung dây chưa nối với tải thì E = U.
Bài tập ví dụ: Từ thông qua một vòng dây dẫn là \(\Phi = \frac{{{{2.10}^{ - 2}}}}{\pi }\cos \left( {100\pi t + \frac{\pi }{4}} \right)\left( {{\rm{W}}b} \right)\). Biểu thức của suất điện động cảm ứng xuất hiện trong vòng dây này là?
Hướng dẫn giải
Ta có:
\(e = - \Phi ' = \omega {\Phi _0}\sin \left( {\omega t + \varphi } \right) \\= \omega {\Phi _0}\cos \left( {\omega t + \varphi - \frac{\pi }{2}} \right)\)
\( \Rightarrow e = \frac{{{{2.10}^{ - 2}}}}{\pi }.100\pi \cos \left( {100\pi t + \frac{\pi }{4} - \frac{\pi }{2}} \right) \\= 2\cos \left( {100\pi t - \frac{\pi }{4}} \right)\left( V \right)\)
Dạng 2: Xác định các đại lượng đặc trưng của dòng điện xoay chiều
- Phương trình tổng quát của dòng điện xoay chiều:
\(i = {I_0}\cos \left( {\omega t + \varphi } \right)\), với I0 là cường độ dòng điện cực đại.
- Các giá trị hiệu dụng:
+ Cường độ dòng điện hiệu dụng: \(I = \frac{{{I_0}}}{{\sqrt 2 }}\)
+ Suất điện động hiệu dụng: \(E = \frac{{{E_0}}}{{\sqrt 2 }}\)
+ Điện áp hiệu dụng: \(U = \frac{{{U_0}}}{{\sqrt 2 }}\)
- Nhiệt lượng tỏa ra trên điện trở R: \(Q = {I^2}Rt\)
Trong đó:
Q: nhiệt lượng (J)
R: điện trở mạch ngoài
t: thời giam dòng điện chạy qua R (s)
- Công suất tỏa nhiệt: \(P = \frac{Q}{t} = {I^2}R\) (W)
Bài tập ví dụ:
Cường độ dòng điện \(i = 2\sqrt 2 \cos \left( {100\pi t} \right)\left( A \right)\) có giá trị hiệu dụng là bao nhiêu?
Hướng dẫn giải
Từ phương trình ta có cường độ dòng điện cực đại \({I_0} = 2\sqrt 2 A\)
Cường độ dòng điện hiệu dụng:
\(I = \frac{{{I_0}}}{{\sqrt 2 }} = \frac{{2\sqrt 2 }}{{\sqrt 2 }} = 2A\)
Dạng 3: Tìm điện lượng chuyển qua tiết diện dây dẫn
Điện lượng qua tiết diện S trong thời gian t là q: \(q = i.t\)
Điện lượng qua tiết diện S trong thời gian từ t1 đến t2 là \(\Delta q\): \(\Delta q = i.\Delta t\)
\( \Rightarrow i = \dfrac{{dq}}{{dt}} \Rightarrow q = \int\limits_{{t_1}}^{{t_2}} {i{\rm{d}}t} \)
Bài tập ví dụ:
Dòng điện xoay chiều có biểu thức: \(i = 2\sin 100\pi t\left( A \right)\) chạy qua dây dẫn. Điện lượng chạy qua tiết diện dây trong khoảng thời gian từ 0 đến 0,15 s là:
Hướng dẫn giải
Ta có:
\( \Rightarrow i = \dfrac{{dq}}{{dt}} \Rightarrow q = \int\limits_{{t_1}}^{{t_2}} {i{\rm{d}}t} = \int\limits_0^{0,15} {2\sin 100\pi tdt} \)
\( \Rightarrow q = - \dfrac{{2\cos 100\pi t}}{{100\pi }}\left| {_0^{0,15}} \right. = \dfrac{4}{{100\pi }}\left( C \right)\)
Dạng 4: Tính số lần dòng điện đổi chiều sau một khoảng thời gian t
Trong mỗi giây: Dòng điện đổi chiều 2f lần
=> Trong thời gian t giây: Dòng điện đổi chiều t.2f lần
Đặc biệt: Nếu pha ban đầu \({\varphi _i} = \frac{\pi }{2}\) hoặc \({\varphi _i} = - \frac{\pi }{2}\)thì chỉ giây đầu tiên đổi chiều 2f-1 lần
Dạng 5: Xác định thời gian đèn sáng - tắt.
- Dùng mối liên hệ giữa dao động điều hòa và chuyển động tròn đều để tính.
- Dòng điện xoay chiều:
- Mỗi giây dòng điện đôi chiều 2f lần.
- Nếu cho dòng điện qua bộ phận làm rung dây trong hiện tượng sóng dừng thì dây rung với tần số 2f.
- Công thức tính thời gian đèn huỳnh quang sáng trong 1 chu kì.
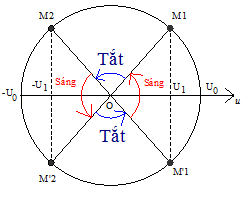
Khi đặt điện áp u = U0cos(wt + ju) vào hai đầu bóng đèn, biết đèn chỉ sáng lên khi u ≥ U1.
\(\Delta t = \frac{{4\Delta \varphi }}{\omega }\) Với \(c{\rm{os}}\Delta \varphi = \frac{{{U_1}}}{{{U_0}}}\),\((0{\rm{ }} < \Delta \varphi < \frac{\pi }{2})\)
