1. TÍCH CỦA VECTO VỚI MỘT SỐ
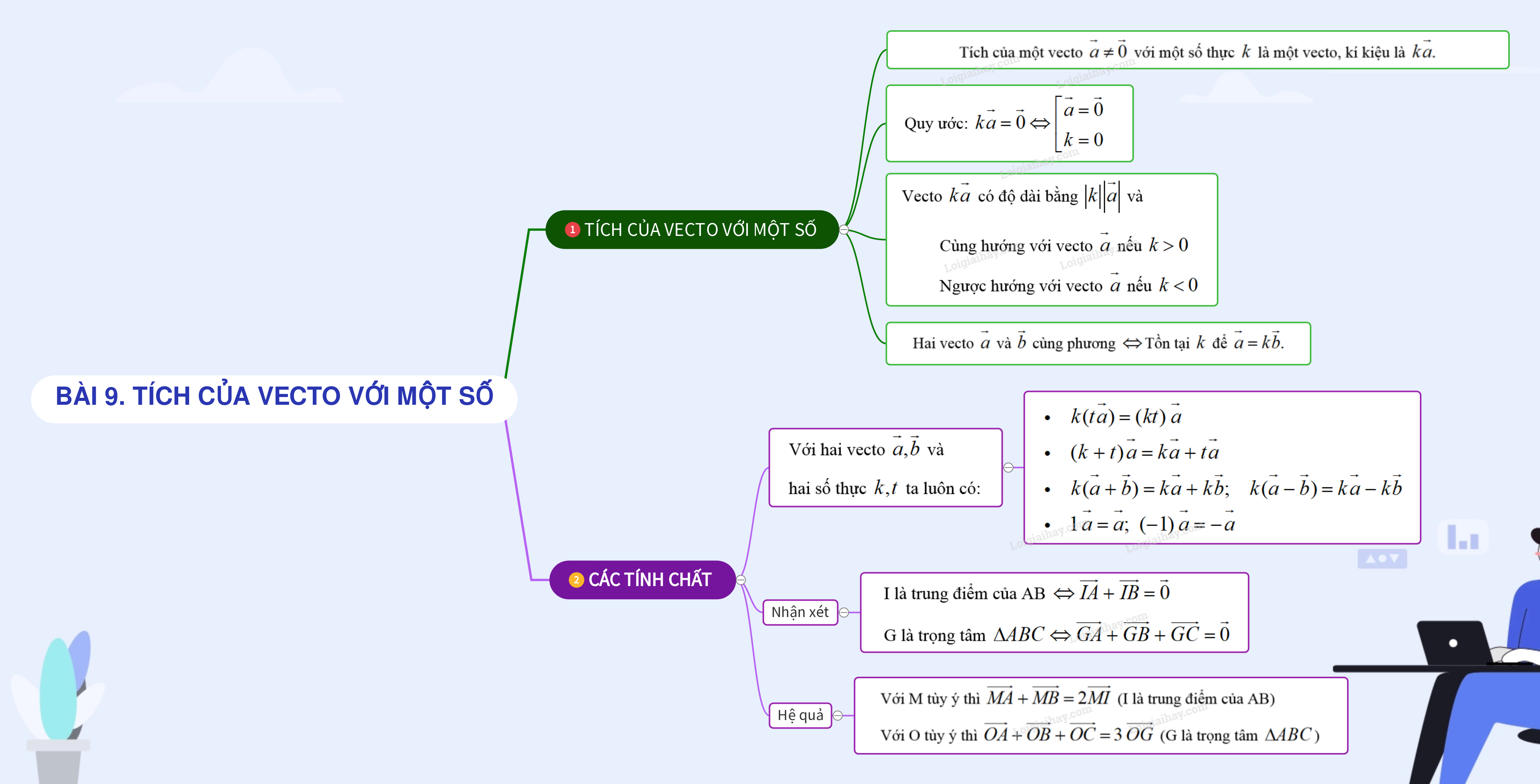
+) Tích của một vecto \(\overrightarrow a \ne \overrightarrow 0 \) với một số thực \(k\) là một vecto, kí kiệu là \(k\overrightarrow a .\)
+) Vecto \(k\overrightarrow a \) có độ dài bằng \(\left| k \right|\left| {\overrightarrow a } \right|\) và
Cùng hướng với vecto \(\overrightarrow a \) nếu \(k > 0\)
Ngược hướng với vecto \(\overrightarrow a \) nếu \(k < 0\)
+) Quy ước: \(k\overrightarrow a = \overrightarrow 0 \Leftrightarrow \left[ \begin{array}{l}\overrightarrow a = \overrightarrow 0 \\k = 0\end{array} \right.\)
Nhận xét: Hai vecto \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương khi và chỉ khi tồn tại \(k\) để \(\overrightarrow a = k\overrightarrow b .\)
2. CÁC TÍNH CHẤT CỦA PHÉP NHÂN VECTƠ VỚI MỘT SỐ
+) Với hai vecto \(\overrightarrow a ,\overrightarrow b \) và hai số thực \(k,t\) ta luôn có:
\(\begin{array}{l}k(t\overrightarrow a ) = (kt)\;\overrightarrow a \\(k + t)\,\overrightarrow a = k\overrightarrow a + t\overrightarrow a \\k(\overrightarrow a + \overrightarrow b ) = k\overrightarrow a + k\overrightarrow b ;\quad k(\overrightarrow a - \overrightarrow b ) = k\overrightarrow a - k\overrightarrow b \\1\;\overrightarrow a = \overrightarrow a ;\;\;( - 1)\;\overrightarrow a = - \,\overrightarrow a \end{array}\)
+) Nhận xét:
I là trung điểm của AB \( \Leftrightarrow \overrightarrow {IA} + \overrightarrow {IB} = \overrightarrow 0 \)
G là trọng tâm \(\Delta ABC \Leftrightarrow \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \)
+) Hệ quả
Với M tùy ý thì \(\overrightarrow {MA} + \overrightarrow {MB} = 2\overrightarrow {MI} \) (I là trung điểm của AB)
Với O tùy ý thì \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = 3\;\overrightarrow {OG} \) (G là trọng tâm \(\Delta ABC\))