Câu 16
Tam giác \(ABC\) vuông tại \(A\) có \(AB = 3cm\), \(AB = 2cm\). Tam giác \(DEF\) vuông tại \(D\) có \(DF = 4cm,DE = x\,cm\). Hai tam giác vuông \(ABC\) và \(DEF\) (h.41) đồng dạng với nhau nếu \(x\) bằng:
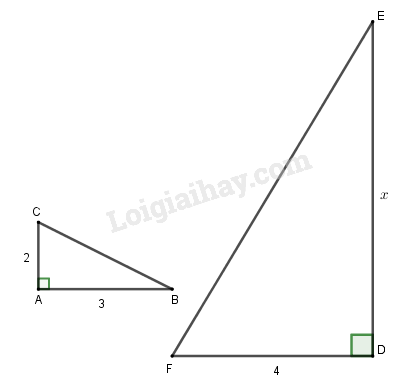
A. \(4\) B. \(5\)
C. \(6\) D. \(7\)
Khoanh tròn vào chữ cái đứng trước khẳng định đúng.
Phương pháp giải:
Xét hai tam giác đồng dạng, từ đó suy ra tỉ số các cạnh và tính \(x\).
Lời giải chi tiết:
\(\Delta ABC \backsim \Delta DEF\) \( \Rightarrow \dfrac{{AB}}{{DE}} = \dfrac{{AC}}{{DF}}\) (tính chất tam giác đồng dạng)
\( \Rightarrow \dfrac{3}{x} = \dfrac{2}{4} \Rightarrow x = \dfrac{{3.4}}{2} = 6\).
Chọn C.
Câu 17
Cho ba tam giác vuông \(ABC,DEF,PMN\) với kích thước các cạnh (cùng đơn vị đo) ghi trên hình 42.
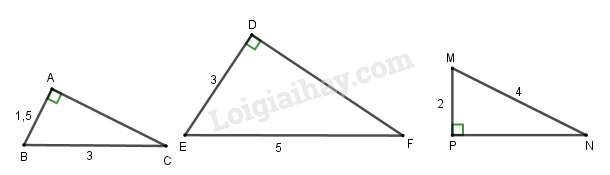
Hai tam giác đồng dạng với nhau là:
A. \(\Delta ABC\) và \(\Delta DEF\)
B. \(\Delta DEF\) và \(\Delta PMN\)
C. \(\Delta PMN\) và \(\Delta ABC\)
Phương pháp giải:
Tính độ dài cạnh còn lại của tam giác \(DEF\) bằng định lí Pi – ta – go rồi sử dụng trường hợp đồng dạng của tam giác vuông để nhận xét.
Lời giải chi tiết:
Tam giác \(DEF\) vuông tại \(D\) nên \(D{F^2} = E{F^2} - D{E^2}\) \( = {5^2} - {3^2} = 16\) \( \Rightarrow DF = 4\)
Xét tam giác \(ABC\) và \(DEF\) có \(\dfrac{{1,5}}{3} \ne \dfrac{3}{5}\) và \(\dfrac{{1,5}}{3} \ne \dfrac{4}{5}\) nên hai tam giác không thể đồng dạng. Loại A.
Xét tam giác \(PMN\) và \(DEF\) có \(\dfrac{2}{3} \ne \dfrac{4}{5}\) và \(\dfrac{2}{4} \ne \dfrac{4}{5}\) nên hai tam giác không thể đồng dạng. Loại B.
Xét tam giác \(PMN\) và \(ABC\) có \(\dfrac{PM}{AB} = \dfrac{MN}{BC}(\,=\dfrac{4}{3})\) và \(\widehat A=\widehat P (\,=90^0)\) nên \( \Delta PMN \backsim \Delta ABC\)
Chọn C.
Câu 18
Cho biết \(\Delta ABC \backsim \Delta DEF\) theo tỉ số đồng dạng \(k = \dfrac{1}{2}\), diện tích tam giác \(ABC\) là: \(13,15c{m^2}\). Khi đó diện tích tam giác \(DEF\) bằng:
A. \(27,30c{m^2}\) B. \(6,58c{m^2}\)
C. \(52,60c{m^2}\)
Khoanh tròn vào chữ cái trước khẳng định đúng.
Phương pháp giải:
Sử dụng tính chất: Tỉ số diện tích của hai tam giác đồng dạng bằng bình phương tỉ số đồng dạng.
Lời giải chi tiết:
\(\Delta ABC \backsim \Delta DEF\) theo tỉ số đồng dạng \(k = \dfrac{1}{2}\)
\( \Rightarrow \dfrac{{{S_{ABC}}}}{{{S_{DEF}}}} = {k^2} = {\left( {\dfrac{1}{2}} \right)^2} = \dfrac{1}{4}\) \( \Rightarrow \dfrac{{13,15}}{{{S_{DEF}}}} = \dfrac{1}{4}\) \( \Rightarrow {S_{DEF}} = 13,15.4 = 52,6c{m^2}\)
Chọn C.
