Câu 21
Một lục giác đều nội tiếp đường tròn bán kính R.
Tỉ số độ dài của cạnh lục giác đều với độ dài của cung bị căng là:
(A) 1 : 6 (B) \(1\,\,:\,\,\pi \)
(C) \(3\,\,:\,\,\pi \) (D) \(6\,\,:\,\,\pi \)
Khoanh tròn vào chữ cái trước kết quả đúng.
Phương pháp giải:
+ Xác định độ dài cạnh của lục giác đều
+ Tính độ dài cung bị căng theo công thức \(l = \dfrac{{\pi Rn}}{{180}}\) với \(n^\circ \) là số đo cung bị căng.
Lời giải chi tiết:
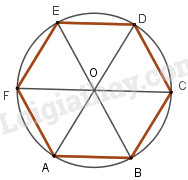
Vì các cạnh của lục giác đều bằng nhau nên ta có 6 cung bằng nhau và số đo mỗi cung bằng \(\dfrac{{360^\circ }}{6} = 60^\circ .\)
Khi đó, độ dài cung nhỏ \(AB\) là \({l_{AB}} = \dfrac{{\pi R.60}}{{180}} = \dfrac{{\pi R}}{3}\)
Lại có \(\widehat {AOB} = 60^\circ \) (=sđ\(\overparen{AB}\))
mà tam giác \(OAB\) cân tại \(O\) (do \(OA = OB\)) suy ra \(OAB\) là tam giác đều
Từ đó \(AB = OA = R.\)
Tỉ số cần tìm là \(AB:{l_{AB}} = R:\dfrac{{\pi R}}{3} = 3:\pi \).
Chọn C.
Câu 22
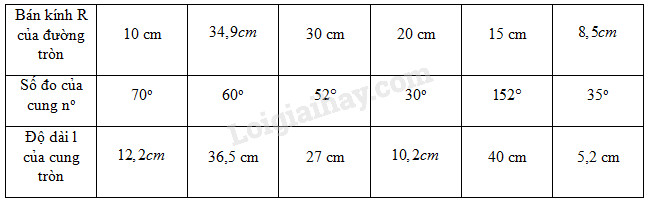
Lấy giá trị gần đúng của \(\pi \) bằng 3,14. Hãy điền vào ô trống (…) trong bảng sau (làm tròn đến chữ số thập phân thứ nhất và đến độ):

Phương pháp giải:
Sử dụng công thức tính độ dài cung \(l = \dfrac{{\pi Rn}}{{180}}\) với \(n^\circ \) là số đo cung và \(R\) là bán kính đường tròn.
Từ đó suy ra \(n = \dfrac{{180l}}{{\pi R}};\,R = \dfrac{{180l}}{{\pi n}}\) .
Lời giải chi tiết:
+ \(R = 10cm;n = 70 \Rightarrow l = \dfrac{{\pi Rn}}{{180}}\)\( = \dfrac{{3,14.10.70}}{{180}} \approx 12,2cm\)
+ \(n = 60;\,l = 36,5 \Rightarrow R = \dfrac{{180l}}{{\pi n}}\)\( = \dfrac{{180.36,5}}{{3,14.60}} \approx 34,9cm\)
+ \(R = 30cm;l = 27cm \Rightarrow n = \dfrac{{180l}}{{\pi R}}\)\( = \dfrac{{180.27}}{{3,14.30}} \approx 52\)
+ \(R = 20cm;n = 30 \Rightarrow l = \dfrac{{\pi Rn}}{{180}}\)\( = \dfrac{{3,14.20.30}}{{180}} \approx 10,5cm\)
+ \(R = 15cm;l = 40cm \Rightarrow n = \dfrac{{180l}}{{\pi R}}\)\( = \dfrac{{180.40}}{{3,14.15}} \approx 152\)
+ \(n = 35;l = 5,2cm \Rightarrow R = \dfrac{{180l}}{{\pi n}}\)\( = \dfrac{{180.5,2}}{{3,14.35}} \approx 8,5cm\)
soanvan.me
