Câu 1
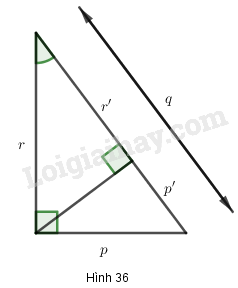
Cho hình 36. Hãy viết hệ thức giữa:
a) Cạnh huyền, cạnh góc vuông và hình chiếu của nó trên cạnh huyền.
b) Các cạnh góc vuông \(p, r\) và đường cao h.
c) Đường cao h và hình chiếu của các cạnh góc vuông trên cạnh huyền \(p', r' \)
Phương pháp giải:
Áp dụng hệ thức lượng trong tam giác vuông
Lời giải chi tiết:
\(\begin{array}{l}
a)\,{p^2} = p'.q;\,{r^2} = r'.q\\
b)\,\dfrac{1}{{{h^2}}} = \dfrac{1}{{{p^2}}} + \dfrac{1}{{{r^2}}}\\
c)\,{h^2} = p'.r'
\end{array}\)
Câu 2
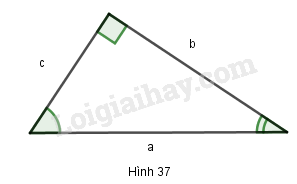
Cho hình 37.
a) Hãy viết công thức tính các tỉ số lượng giác của góc \(α\)
b) Hãy viết hệ thức giữa các tỉ số lượng giác của góc \(α\) và các tỉ số lượng giác của góc \(β.\)
Lời giải chi tiết:
\(\begin{array}{l}
a)\,\sin \alpha = \dfrac{b}{a};\,\cos \alpha = \dfrac{c}{a};\,\tan \alpha = \dfrac{b}{c};\cot \,\alpha = \dfrac{c}{b}\\
b)\,\sin \alpha = \cos \beta ;\,\cos \alpha = \sin \beta \\
\tan \alpha = \cot \beta ;\cot \alpha = \tan \beta
\end{array}\)
Câu 3
Xem hình 37.
a) Hãy viết công thức tính các cạnh góc vuông b và c theo cạnh huyền a và tỉ số lượng giác của các góc \(α, β.\)
b) Hãy viết công thức tính mỗi cạnh góc vuông theo cạnh góc vuông kia và tỉ số lượng giác của các góc \(α, β.\)
Lời giải chi tiết:
a) Ta có:
\(b = a\sin α = a\cosβ;\) \( c = a\sinβ = a\cosα\)
b) \(b = c.\tanα = c.\cotβ\)
\(c = b.\tan β= b.\cot α\)
Câu 4
Để giải một tam giác vuông, cần biết ít nhất mấy góc và cạnh? Có lưu ý gì về số cạnh?
Lời giải chi tiết:
Để giải một tam giác vuông cần biết hai yếu tố trong đó có ít nhất là một yếu tố cạnh.
soanvan.me
