Cho đoạn mạch gồm điện trở\({R_1}\) mắc song song với điện trở \({R_2}\) mắc vào mạch điện. Gọi \(U,{U_1},{U_2}\) lần lượt là hiệu điện thế qua \({R_1},{R_2}\). Biểu thức nào sau đây đúng?
-
A
\(U = {U_1} = {U_2}\)
-
B
\(U = {U_1} + {U_2}\)
-
C
\(U \ne {U_1} = {U_2}\)
-
D
\({U_1} \ne {U_2}\)
Đáp án của giáo viên lời giải hay : A
Ta có, trong đoạn mạch mắc song song thì:
Hiệu điện thế hai đầu đoạn mạch song song bằng hiệu điện thế hai đầu mỗi đoạn mạch rẽ.
\(U = {U_1} = {U_2} = \ldots = {U_n}\)
Phát biểu nào dưới đây không đúng đối với đoạn mạch gồm các điện trở mắc song song?
-
A
Cường độ dòng điện trong mạch chính bằng tổng cường độ dòng điện trong các mạch rẽ.
-
B
Hiệu điện thế giữa hai đầu đoạn mạch bằng tổng các hiệu điện thế giữa hai đầu mỗi điện trở mắc trong đoạn mạch.
-
C
Hiệu điện thế giữa hai đầu đoạn mạch bằng hiệu điện thế giữa hai đầu mỗi điện trở mắc trong đoạn mạch
-
D
Hiệu điện thế giữa hai đầu mỗi điện trở mắc trong đoạn mạch tỉ lệ thuận với điện trở đó.
Đáp án của giáo viên lời giải hay : B
A, C, D - đúng
B - sai vì: Hiệu điện thế hai đầu đoạn mạch song song bằng hiệu điện thế hai đầu mỗi đoạn mạch rẽ: \(U = {U_1} = {U_2} = \ldots = {U_n}\)
Biểu thức nào sau đây xác định điện trở tương đương của đoạn mạch có hai điện trở \({R_1},{R_2}\) mắc song song?
-
A
\(\frac{1}{{{R_{t{\rm{d}}}}}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}\)
-
B
\({R_{t{\rm{d}}}} = \frac{{{R_1}{R_2}}}{{{R_1} - {R_2}}}\)
-
C
\({R_{t{\rm{d}}}} = {R_1} + {R_2}\)
-
D
\({R_{t{\rm{d}}}} = \left| {{R_1} - {R_2}} \right|\)
Đáp án của giáo viên lời giải hay : A
Ta có:
Nghịch đảo điện trở tương đương của đoạn mạch song song bằng tổng các nghịch đảo điện trở các đoạn mạch rẽ: $\frac{1}{{{R_{t{\text{d}}}}}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}$
Đặt một hiệu điện thế \({U_{AB}}\) vào hai đầu đoạn mạch gồm hai điện trở \({R_1}\) và \({R_2}\) mắc song song. Hiệu điện thế giữa hai đầu mỗi điện trở tương ứng là \({U_1},{U_2}\). Hệ thức nào sau đây là đúng?
-
A
\({R_{AB}} = {R_1} + {R_2}\)
-
B
\({I_{AB}} = {I_1} = {I_2}\)
-
C
\(\frac{{{I_1}}}{{{I_2}}} = \frac{{{R_2}}}{{{R_1}}}\)
-
D
\({U_{AB}} = {U_1} + {U_2}\)
Đáp án của giáo viên lời giải hay : C
A - sai vì: \(\frac{1}{{{R_{AB}}}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}\)
B - sai vì: \({I_{A{\bf{B}}}} = {I_1} + {I_2}\)
C - đúng
D - sai \({U_{AB}} = {U_1} = {U_2}\)
Cho hai điện trở \({R_1} = {R_2} = 20\Omega \). Được mắc như sơ đồ
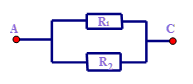
Điện trở tương đương của đoạn mạch AC có giá trị là:
-
A
\(20\Omega \)
-
B
\(40\Omega \)
-
C
\(10\Omega \)
-
D
\(80\Omega \)
Đáp án của giáo viên lời giải hay : C
Sử dụng biểu thức tính điện trở tương đương của đoạn mạch có các điện trở song song: \(\frac{1}{{{R_{t{\rm{d}}}}}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}\)
Điện trở tương đương của đoạn mạch được tính theo công thức
\(\frac{1}{{{R_{12}}}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}} = \frac{1}{{20}} + \frac{1}{{20}} = \frac{1}{{10}} \to {R_{12}} = {\rm{ }}10\Omega \)
Nếu mắc thêm điện trở \({R_3} = 15\Omega \) vào đoạn mạch trên như sơ đồ (2) thì điện trở tương đương RAC của đoạn mạch mới là bao nhiêu ? So sánh điện trở RAC với mỗi điện trở thành phần ?
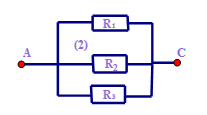
-
A
${R_{AC}} = 25\Omega $ và lớn hơn điện trở thành phần
-
B
\({R_{AC}} = 6\Omega \) và nhỏ hơn điện trở thành phần
-
C
\({R_{AC}} = 55\Omega \) và lớn hơn điện trở thành phần
-
D
\({R_{AC}} = 10\Omega \) và nhỏ hơn điện trở thành phần
Đáp án của giáo viên lời giải hay : B
Sử dụng biểu thức tính điện trở tương đương của đoạn mạch có các điện trở song song: \(\frac{1}{{{R_{t{\rm{d}}}}}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}\)
Khi mắc thêm điện trở \({R_3}\) ( như sơ đồ 2) , ta có \({R_{AC}} = \frac{{{R_{12}}{R_3}}}{{{R_{12}} + {R_3}}} = \frac{{10\,.\,15}}{{10 + 15}} = 6\Omega \)
Nhận xét : \({R_{AC}}\) nhỏ hơn điện trở thành phần
Cho mạch điện có sơ đồ như hình bên trong đó điện trở \({R_1} = 18\Omega ,{R_2} = 12\Omega \). Vôn kế chỉ \(36V\)
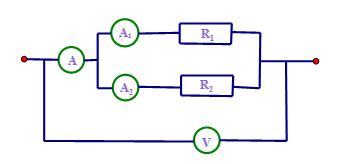
Số chỉ của ampe kế \({A_1}\) là:
-
A
1,2A
-
B
3A
-
C
5A
-
D
2A
Đáp án của giáo viên lời giải hay : D
+ Vận dụng biểu thức xác định hiệu điện thế trong đoạn mạch mắc song song: \(U = {U_1} = {U_2} = ...\)
+ Áp dụng biểu thức định luật Ôm: \(I = \frac{U}{R}\)
+ Hiệu điện thế của hai đầu đoạn mạch bằng hiệu điện thế giữa các đoạn mạch
\(U = {U_1} = {U_2}\)
+ Số chỉ của ampe kế \({A_1}\) là cường độ dòng điện đi qua điện trở \({R_1}\)
Vậy số chỉ của ampe kế \({A_1}\) là: \({{\rm{I}}_{\rm{1}}} = \frac{U}{{{R_1}}} = \frac{{36}}{{18}} = 2{\rm{A}}\)
Cho mạch điện có sơ đồ như hình bên trong đó điện trở \({R_1} = 15\Omega ,{R_2} = 10\Omega \). Ampe kế \({A_1}\) chỉ \(0,5A\)
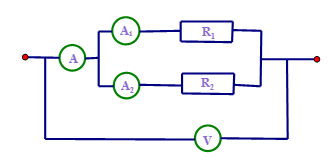
Số chỉ của vôn kế là:
-
A
$7,5V$
-
B
$5V$
-
C
$12,5V$
-
D
$3V$
Đáp án của giáo viên lời giải hay : A
+ Vận dụng biểu thức xác định hiệu điện thế trong đoạn mạch mắc song song: \(U = {U_1} = {U_2} = ...\)
+ Vận dụng biểu thức tính hiệu điện thế: \(U = IR\)
+ Vì hai điện trở \({R_1}\) và \({R_2}\) mắc song song nên \(U = {U_1} = {U_2}\)
+ Vậy số chỉ của vôn kế là \(U = {U_1} = {I_1}{R_1} = 0,5.15 = 7,5{\rm{ }}V\)
Tính số chỉ của ampe kế A
-
A
$0,5A$
-
B
$1,25A$
-
C
$2A$
-
D
$1,5A$
Đáp án của giáo viên lời giải hay : B
+ Áp dụng biểu thức định luật Ôm: \(I = \dfrac{U}{R}\)
+ Vận dụng biểu thức tính cường độ dòng điện trong đoạn mạch có các điện trở mắc nối tiếp:
\(I = {I_1} + {I_2}\)
+ Số chỉ của ampe kế \({A_2}\) là \({{\rm{I}}_{\rm{2}}} = \dfrac{U}{{{R_2}}} = \dfrac{{7,5}}{{10}} = 0,75{\rm{A}}\)
+ Số chỉ của ampe kế \(A\) là: \(I = {I_1} + {I_2} = 0,5{\rm{ }} + 0,75 = 1,25{\rm{ }}A\)
Cho mạch điện có sơ đồ như hình bên trong đó điện trở \({R_1} = 52,5\Omega \). Vôn kế chỉ \(84V\). Ampe kế A chỉ \(4,2A\). Điện trở \({R_2} = ?\)
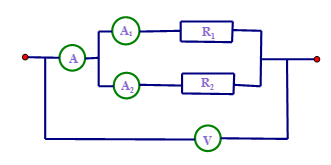
-
A
\(52,5\Omega \)
-
B
\(32,3\Omega \)
-
C
\(20\Omega \)
-
D
\(21\Omega \)
Đáp án của giáo viên lời giải hay : B
+ Áp dụng biểu thức định luật Ôm: \(I = \frac{U}{R}\)
+ Vận dụng biểu thức tính cường độ dòng điện trong đoạn mạch có các điện trở mắc nối tiếp:
\(I = {I_1} + {I_2}\)
+ Số chỉ của ampe kế A1 là \({{\rm{I}}_{\rm{1}}} = \dfrac{U}{{{R_1}}} = \dfrac{{84}}{{52,5}} = 1,6{\rm{A}}\)
+ Số chỉ của ampe kế A2 là \({I_2} = I-{I_1} = 4,2-1,6 = 2,6A\)
+ Điện trở R2 là \({{\rm{R}}_{\rm{2}}} = \dfrac{U}{{{I_2}}} = \dfrac{{84}}{{2,6}} = 32,3\Omega \)
Cho mạch điện có sơ đồ như hình bên . Hiệu điện thế \(U = 48V\). Biết rằng:
- Khi khóa \({K_1}\) đóng, khóa \({K_2}\) mở thì ampe kế chỉ \(2,4A\)
- Khi khóa \({K_1}\) mở, khóa \({K_2}\) đóng thì ampe kế chỉ \(5A\)
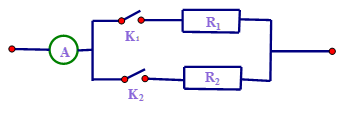
Tính điện trở \({R_1},{R_2}\)?
-
A
\({R_1} = 2\Omega ;{R_2} = 9,6\Omega \)
-
B
\({R_1} = 20\Omega ;{R_2} = 96\Omega \)
-
C
\({R_1} = 20\Omega ;{R_2} = 9,6\Omega \)
-
D
\({R_1} = 100\Omega ;{R_2} = 96\Omega \)
Đáp án của giáo viên lời giải hay : C
+ Vận dụng biểu thức xác định hiệu điện thế trong đoạn mạch mắc song song: \(U = {U_1} = {U_2} = ...\)
+ Vận dụng biểu thức tính cường độ dòng điện trong đoạn mạch có các điện trở mắc song song:
\(I = {I_1} + {I_2}\)
- Khi khóa \({K_1}\) đóng , khóa \({K_2}\) mở thì ampe kế chỉ \(2,4A\) thì dòng điện chỉ đi qua điện trở \({R_1}\)
Cho nên điện trở \({R_1}\) là \({{\rm{R}}_{\rm{1}}} = \dfrac{U}{{{I_1}}} = \dfrac{{48}}{{2,4}} = 20\Omega \)
- Khi khóa \({K_1}\) mở , khóa \({K_2}\) đóng thì ampe kế chỉ \(5A\) thì dòng điện chỉ đi qua điện trở \({R_2}\)
Cho nên điện trở \({R_2}\) là \({{\rm{R}}_{\rm{2}}} = \dfrac{U}{{{I_2}}} = \dfrac{{48}}{5} = 9,6\Omega \)
Khi cả hai khóa cùng đóng thì ampe kế chỉ bao nhiêu ?
-
A
5A
-
B
7,4A
-
C
2,4A
-
D
3,7A
Đáp án của giáo viên lời giải hay : B
+ Vận dụng biểu thức xác định hiệu điện thế trong đoạn mạch mắc song song: \(U = {U_1} = {U_2} = ...\)
+ Vận dụng biểu thức tính cường độ dòng điện trong đoạn mạch có các điện trở mắc song song: \(I = {I_1} + {I_2}\)
Vì cùng hiệu điện thế U , nên khi hai khóa cùng đóng thì số chỉ của ampe kế là:
\(I = {I_1} + {I_2} = 2,4 + 5 = 7,4A\)
Cho mạch điện có sơ đồ như hình bên . Hiệu điện thế \({U_{AB}} = 48V\). Biết \({R_1} = 16\Omega ,{R_2} = 24\Omega \). Khi mắc thêm điện trở \({R_3}\) vào hai điểm C và D thì ampe kế chỉ \(6A\). Hãy tính điện trở \({R_3}\)?
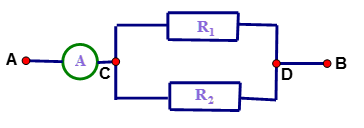
-
A
\({R_3} = 16\Omega \)
-
B
\({R_3} = 48\Omega \)
-
C
\({R_3} = 24\Omega \)
-
D
\({R_3} = 32\Omega \)
Đáp án của giáo viên lời giải hay : B
+ Vận dụng biểu thức xác định hiệu điện thế trong đoạn mạch mắc song song: \(U = {U_1} = {U_2} = ...\)
+ Sử dụng biểu thức định luật Ôm tính cường độ dòng điện qua mỗi điện trở: \(I = \frac{U}{R}\)
+ Vận dụng biểu thức tính cường độ dòng điện trong đoạn mạch có các điện trở mắc song song: \(I = {I_1} + {I_2}\)
Cường độ dòng điện qua mỗi điện trở là:
\({{\rm{I}}_{\rm{1}}} = \dfrac{U}{{{R_1}}} = \dfrac{{48}}{{16}} = 3{\rm{A}}\) ; \({{\rm{I}}_{\rm{2}}} = \dfrac{U}{{{R_2}}} = \dfrac{{48}}{{24}} = 2{\rm{A}}\)
Số chỉ của ampe kế là \(I = {I_1} + {I_2} = 2 + 3 = 5A\)
Khi mắc thêm điện trở \({R_3}\) vào hai đầu đoạn mạch CD thì các điện trở \({R_1},{R_2},{R_3}\) mắc song song , cho nên cường độ dòng điện qua điện trở \({R_3}\) là \({I_3} = I'-\left( {{I_1} + {I_2}} \right) = 6-\left( {2 + 3} \right) = 1A\)
Giá trị của điện trở \({R_3}\) là: \({{\text{R}}_{\text{3}}} = \dfrac{U}{{{I_3}}} = \dfrac{{48}}{1} = 48\Omega \)
Một đoạn mạch gồm ba điện trở \({R_1} = 9\Omega ,{R_2} = 18\Omega \) và \({R_3} = 24\Omega \) được mắc vào hiệu điện thế $U = 3,6V$ như sơ đồ bên
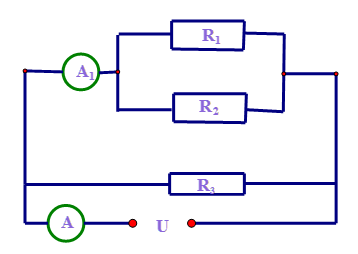
Số chỉ của ampe kế A và A1 là:
-
A
0,5A và 0,4A
-
B
0,6A và 0,35A
-
C
0,75A và 0,6A
-
D
0,07A và 0,13A
Đáp án của giáo viên lời giải hay : C
+ Sử dụng biểu thức tính điện trở tương đương trong đoạn mạch có các điện trở mắc song song:
\(\dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + ...\)
+ Áp dụng biểu thức định luật Ôm tính cường độ dòng điện: \(I = \dfrac{U}{R}\)
+ Điện trở tương đương của đoạn mạch gồm \({R_1}\) và \({R_2}\) mắc song song là \({{\rm{R}}_{{\rm{12}}}} = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} = \dfrac{{9.18}}{{9 + 18}} = 6\Omega \)
Điện trở tương đương của đoạn mạch là \({{\rm{R}}_{{\rm{123}}}} = \dfrac{{{R_{12}}{R_3}}}{{{R_{12}} + {R_3}}} = \dfrac{{6.24}}{{6 + 24}} = 4,8\Omega \)
+ Số chỉ của ampe kế A là \(I = \dfrac{U}{{{R_{123}}}} = \dfrac{{3,6}}{{4,8}} = 0,75{\rm{A}}\)
Số chỉ của ampe kế A1 là \({{\rm{I}}_{\rm{1}}} = \dfrac{U}{{{R_{12}}}} = \dfrac{{3,6}}{6} = 0,6{\rm{A}}\)
Cho một hiệu điện thế \(U = 1,8V\) và hai điện trở \({R_1},{R_2}\). Nếu mắc nối tiếp hai điện trở vào hiệu điện thế \(U\) thì dòng điện đi qua chúng có cường độ \({I_1} = 0,2{\rm{ }}A\); nếu mắc song song hai điện trở vào hiệu điện thế \(U\) thì dòng điện mạch chính có cường độ \({I_2} = 0,9A\) . Tính \({R_1},{\rm{ }}{R_2}\)?
-
A
\({R_1} = 3\Omega ,{R_2} = 6\Omega \)
-
B
\({R_1} = 2\Omega ,{R_2} = 4\Omega \)
-
C
\({R_1} = 2\Omega ,{R_2} = 9\Omega \)
-
D
\({R_1} = 3\Omega ,{R_2} = 9\Omega \)
Đáp án của giáo viên lời giải hay : A
+ Sử dụng biểu thức tính tổng trở của đoạn mạch mắc nối tiếp: \({R_{nt}} = {R_1} + {R_2}\)
+ Sử dụng biểu thức tính tổng trở của đoạn mạch mắc song song: \(\frac{1}{{{R_{//}}}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}\)
+ Khi \({R_1},{R_2}\) mắc nối tiếp nên \({R_1} + {R_2} = \dfrac{U}{{{I_1}}} = \dfrac{{1,8}}{{0,2}} = 9\Omega \) (1)
+ Khi \({R_1},{R_2}\) mắc song song nên \({R_{12}} = \dfrac{U}{{{I_2}}} = \dfrac{{1,8}}{{0,9}} = 2\Omega \), mà \({{\rm{R}}_{{\rm{12}}}} = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}\)
Cho nên \({R_1}{R_2} = 18\) (2)
Từ (1) ta có \({R_2} = 9-{R_1}\) thay vào (2) ta có :
\(\begin{array}{l}{R_1}\left( {9{\rm{ }}-{\rm{ }}{R_1}} \right) = 18\\ \leftrightarrow {R_1}^2 - 9R_1+18 =0 \leftrightarrow \left( {{R_1}-3} \right)\left( {{R_1}-6} \right) = 0\end{array}\)
\(\left[ \begin{array}{l}{R_1} = 3\Omega \\{R_2} = 6\Omega \end{array} \right. \Rightarrow \left[ \begin{array}{l}{R_2} = 9 - 3 = 6\Omega \\{R_2} = 9 - 6 = 3\Omega \end{array} \right.\)
Vậy \({R_1} = 3\Omega ;{R_2} = 6\Omega \) hoặc \({R_1} = 6\Omega ;{R_2} = 3\Omega \)
Cho hai điện trở, R1 = 15Ω chịu được dòng điện có cường độ tối đa 2A và R2 = 10Ω chịu được dòng điện có cường độ tối đa 1A. Hiệu điện thế tối đa có thể đặt vào hai đầu đoạn mạch gồm R1 và R2 mắc song song là:
-
A
40V
-
B
10V
-
C
30V
-
D
25V
Đáp án của giáo viên lời giải hay : B
Công thức của mạch song song: \(\left\{ \begin{array}{l}U = {U_1} = {U_2}\\I = {I_1} + {I_2}\\{R_{td}} = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}\end{array} \right.\)
Định luật Ôm : \(I = \dfrac{U}{R} \Rightarrow U = I.R\)
Mạch điện gồm \({R_1}\,//\,{R_2} \Rightarrow U = {U_1} = {U_2}\)
Mà : \(\left\{ \begin{array}{l}{U_{1\max }} = {I_{1\max }}{R_1} = 2.15 = 30V \Rightarrow {U_1} \le 30V\\{U_{2\max }} = {I_{2\max }}{R_2} = 1.10 = 10V \Rightarrow {U_2} \le 10V\end{array} \right.\)
\( \Rightarrow \left\{ \begin{array}{l}U \le 30V\\U \le 10V\end{array} \right. \Rightarrow U \le 10V \Rightarrow {U_{\max }} = 10V\)
Hai điện trở R1 = 8Ω , R2 = 2Ω mắc song song với nhau vào hiệu điện thế U = 3,2V . Cường độ dòng điện chạy qua mạch chính là :
-
A
1A
-
B
1,5A
-
C
2,0A
-
D
2,5A
Đáp án của giáo viên lời giải hay : C
+ Mạch mắc song song: \(\left\{ \begin{array}{l}{R_{td}} = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}\\I = {I_1} + {I_2}\\U = {U_1} = {U_2}\end{array} \right.\)
+ Định luật Ôm: \(I = \dfrac{U}{{{R_{td}}}}\)
Điện trở tương đương của đoạn mạch:
\({R_{td}} = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} = \dfrac{{8.2}}{{8 + 2}} = 1,6\Omega \)
Cường độ dòng điện chạy qua mạch chính: \(I = \dfrac{U}{{{R_{td}}}} = \dfrac{{3,2}}{{1,6}} = 2A\)
Có 2 điện trở R1 và R2 (với R1 = R2 = r).Gọi Rnt và Rss lần lượt là điện trở tương đương của chúng khi được mắc nối tiếp và mắc song song. Kết quả nào sau đây là đúng
-
A
Rnt = 2.Rss
-
B
Rnt = 4.Rss
-
C
Rss = 2Rnt
-
D
Rss = 4Rnt
Đáp án của giáo viên lời giải hay : B
Công thức tính điện trở tương đương của đoạn mạch nối tiếp và song song: \(\left\{ \begin{array}{l}{R_{nt}} = {R_1} + {R_2}\\\frac{1}{{{R_{ss}}}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}\end{array} \right.\)
Ta có: \(\left\{ \begin{array}{l}{R_{nt}} = {R_1} + {R_2} = r + r = 2r\\\frac{1}{{{R_{ss}}}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}} = \frac{1}{r} + \frac{1}{r}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{R_{nt}} = 2r\\{R_{ss}} = \frac{r}{2}\end{array} \right. \Rightarrow {R_{nt}} = 4{R_{ss}}\)
Hai điện trở R1, R2 có trị số bằng nhau, đang mắc song song chuyển thành nối tiếp thì điện trở tương đương của mạch sẽ thay đổi thế nào?
-
A
tăng lên 4 lần
-
B
không đổi
-
C
giảm đi 4 lần
-
D
giảm 2 lần
Đáp án của giáo viên lời giải hay : A
Công thức tính điện trở tương đương của mạch mắc nối tiếp và song song: \(\left\{ \begin{array}{l}\frac{1}{{{R_{//}}}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}\\{R_{nt}} = {R_1} + {R_2}\end{array} \right.\)
Hai điện trở R1, R2 có trị số bằng nhau: trở R1= R2 = R
Hai điện trở mắc song song: \(\frac{1}{{{R_{//}}}} = \frac{1}{R} + \frac{1}{R} = \frac{2}{R} \Rightarrow {R_{//}} = \frac{R}{2}\)
Hai điện trở mắc nối tiếp: \({R_{nt}} = R + R = 2R\)
Hai điện trở R1, R2 có trị số bằng nhau, đang mắc song song chuyển thành nối tiếp thì điện trở tương đương của mạch sẽ tăng lên 4 lần
R1 = 10Ω, R2 = 15Ω, R3 = 30Ω mắc song song với nhau. Nhận định nào sau đây là đúng?
-
A
\({I_1}:{I_2}:{I_3} = 1:3:2\)
-
B
\({I_1}:{I_2}:{I_3} = 2:3:1\)
-
C
\({I_1}:{I_2}:{I_3} = 3:2:1\)
-
D
\({I_1}:{I_2}:{I_3} = 1:2:3\)
Đáp án của giáo viên lời giải hay : C
Đoạn mạch gồm ba điện trở mắc song song: \(\left\{ \begin{array}{l}U = {U_1} = {U_2} = {U_3}\\I = {I_1} + {I_2} + {I_3}\end{array} \right.\)
Hệ thức định luật Ôm: \(I = \frac{U}{R}\)
Ba điện trở mắc song song:
\(\begin{array}{l}
{U_1} = {U_2} = {U_3} \Leftrightarrow {I_1}.{R_1} = {I_2}.{R_2} = {I_3}.{R_3}\\
\Leftrightarrow 10{I_1} = 15{I_2} = 30{I_3} \Leftrightarrow 2{I_1} = 3{I_2} = 6{I_3}
\end{array}\)
BCNN (2; 3; 6) = 6 \( \Rightarrow \left\{ \begin{array}{l}{I_1} = 3\\{I_2} = 2\\{I_3} = 1\end{array} \right. \Rightarrow {I_1}:{I_2}:{I_3} = 3:2:1\)
Ba bóng đèn có điện trở bằng nhau, chịu được hiệu điện thế định mức 6V. Phải mắc ba bóng đèn theo kiểu nào vào hai điểm có hiệu điện thế 18V để chúng sáng bình thường?
-
A
ba bóng mắc song song
-
B
hai bóng song song, bóng thứ ba nối tiếp với hai bóng trên
-
C
hai bóng nối tiếp, bóng còn lại song song với cả hai bóng trên
-
D
ba bóng mắc nối tiếp nhau
Đáp án của giáo viên lời giải hay : D
Công thức của mạch mắc nối tiếp: \(\left\{ \begin{array}{l}U = {U_1} + {U_2}\\I = {I_1} = {I_2}\end{array} \right.\)
Công thức của mạch mắc song song: \(\left\{ \begin{array}{l}U = {U_1} = {U_2}\\I = {I_1} + {I_2}\end{array} \right.\)
Hiệu điện thế của mạch: U = 18V
Đèn sáng bình thường thì: \(\left\{ \begin{array}{l}{U_1} = 6V\\{U_2} = 6V\\{U_3} = 6V\end{array} \right.\)
Khi mắc ba bóng đèn mắc nối tiếp với nhau: \(U = {U_1} + {U_2} + {U_3} = 18V\)
Thật vậy: Khi mắc Đ1 nối tiếp Đ2 nối tiếp Đ3 \( \Rightarrow I = {I_1} = {I_2} = {I_3}\) (1)
Mà \({R_1} = {R_2} = {R_3}\) (2)
Từ (1) và (2) suy ra:
\(\begin{array}{l}{U_1} = {U_2} = {U_3} \Rightarrow U = {U_1} + {U_2} + {U_3} = 3{U_1} = 18V \Rightarrow {U_1} = 6V\\ \Rightarrow {U_2} = {U_3} = 6V\end{array}\)
Vậy 3 đèn sáng bình thường.
Có 2 điện trở R1 và R2 (với R1 = R2 = r).Gọi Rnt và Rss lần lượt là điện trở tương đương của chúng khi được mắc nối tiếp và mắc song song. Kết quả nào sau đây là đúng
-
A
Rnt = 2.Rss
-
B
Rnt = 4.Rss
-
C
Rss = 2Rnt
-
D
Rss = 4Rnt
Đáp án của giáo viên lời giải hay : B
Công thức tính điện trở tương đương của đoạn mạch nối tiếp và song song: \(\left\{ \begin{array}{l}{R_{nt}} = {R_1} + {R_2}\\\dfrac{1}{{{R_{ss}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}\end{array} \right.\)
Ta có: \(\left\{ \begin{array}{l}{R_{nt}} = {R_1} + {R_2} = r + r = 2r\\\dfrac{1}{{{R_{ss}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} = \dfrac{1}{r} + \dfrac{1}{r}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{R_{nt}} = 2r\\{R_{ss}} = \dfrac{r}{2}\end{array} \right. \Rightarrow {R_{nt}} = 4{R_{ss}}\)
Cho mạch điện có sơ đồ như hình vẽ, trong đó R1 = 5Ω, R2 = 10Ω, ampe kế A1 chỉ 0,6A. Cường độ dòng điện ở mạch chính là:
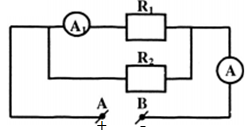
-
A
0,6A
-
B
0,9A
-
C
0,12A
-
D
0,15A
Đáp án của giáo viên lời giải hay : B
Công thức của đoạn mạch gồm các điện trở tương đương: \(\left\{ \begin{array}{l}U = {U_1} = {U_2}\\I = {I_1} + {I_2}\\\dfrac{1}{{{R_{td}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}\end{array} \right.\)
Do hai điện trở mắc song song với nhau hiệu điện thế giữa hai đầu AB của đoạn mạch là:
\({U_{AB}} = {U_1} = {I_1}.{R_1} = 0,6.5 = 3\,\,\left( V \right)\)
Điện trở tương đương của mạch điện: \(\dfrac{1}{{{R_{td}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} \Leftrightarrow \dfrac{1}{{{R_{td}}}} = \dfrac{1}{5} + \dfrac{1}{{10}} \Rightarrow {R_{td}} = \dfrac{{10}}{3}\Omega \)
Cường độ dòng điện ở mạch chính là: \(I = \dfrac{U}{{{R_{td}}}} = \dfrac{3}{{\dfrac{{10}}{3}}} = 0,9A\)
