Đề bài
Phần I. Trắc nghiệm (3 điểm)
Chọn ý đúng ghi vào bài làm.
Câu 1. Số bé nhất trong các số: 3,055; 3,050; 3,005; 3,505 là:
A. 3,505 B. 3,050
C. 3,005 D. 3,055
Câu 2. Trung bình một người thợ làm một sản phẩm hết 1 giờ 30 phút. Người đó làm 5 sản phẩm mất bao lâu?
A. 7 giờ 30 phút B. 7 giờ 50 phút
C. 6 giờ 50 phút D. 6 giờ 15 phút
Câu 3. Có bao nhiêu số thập phân ở giữa 0,5 và 0,6:
A. Không có số nào B. 1 số
C. 9 số D. Rất nhiều số
Câu 4. Hỗn số 3\(\dfrac{9}{{100}}\)viết thành số thập phân là:
A. 3,90 B. 3,09
C. 3,9100 D. 3,109
Câu 5. Tìm một số biết 20% của nó là 16. Số đó là:
A. 0,8 B. 8
C. 80 D. 800
Câu 6. Một hình lập phương có diện tích xung quanh là 36dm2. Thể tích hình lập phương đó là:
A. 27dm3 B. 2700cm3
C. 54dm3 D. 27000cm3
Phần II. Tự luận (7 điểm)
Bài 1. (2 điểm) Đặt tính và tính.
a) 56,72 + 76,17
b) 367,21 – 128,82
c) 3,17 × 4,5
d) 52,08 : 4,2
Bài 2. (1 điểm) Điền số thích hợp vào chỗ chấm:
a) 0,48m2 = …… cm2
b) 0,2kg = …… g
c) 5628dm3 = ……m3
d) 3 giờ 6 phút = ….giờ
Bài 3. (3 điểm) Quãng đường AB dài 180 km. Lúc 7 giờ 30 phút, một ô tô đi từ A đến B với vận tốc 54 km/giờ, cùng lúc đó một xe máy đi từ B đến A với vận tốc 36 km/giờ. Hỏi:
a) Hai xe gặp nhau lúc mấy giờ?
b) Chỗ 2 xe gặp nhau cách A bao nhiêu ki-lô-mét?
Bài 4. Tính nhanh (1 điểm)
\(\dfrac{{13}}{{50}} + 9\% + \dfrac{{41}}{{100}} + 0,24\)
Lời giải
Phần 1. Trắc nghiệm
Câu 1.
Phương pháp:
So sánh các số đã cho, từ đó tìm được số bé nhất trong các số.
Cách giải:
So sánh các số ta có:
3,005 < 3,050 < 3,055 < 3,505.
Vậy số bé nhất trong các số đó là 3,005.
Chọn B.
Câu 2.
Phương pháp:
Thời gian làm 5 sản phẩm = thời gian làm 1 sản phẩm × 5.
Cách giải:
Thời gian người đó làm 5 sản phẩm là:
1 giờ 30 phút × 5 = 5 giờ 150 phút
5 giờ 150 phút = 7 giờ 30 phút
(Vì 150 phút = 2 giờ 30 phút)
Đáp số: 7 giờ 30 phút.
Chọn A.
Câu 3.
Phương pháp:
Áp dụng tính chất về số thập phân bằng nhau và cách so sánh hai số thập phân.
Cách giải:
Ta có: 0,5 = 0,50 = 0,500 = ...
0,6 = 0,60 = 0,600 = ...
Do đó có rất nhiều số thập phân ở giữa 0,5 và 0,6 (chẳng hạn 0,51; 052; 0,53; ...; 0,501; 0,502; 0,503 ; ...; )
Chọn D.
Câu 4.
Phương pháp:
Áp dụng cách viết: \(\dfrac{1}{{100}} = 0,01\).
Cách giải:
Ta có: \(3\dfrac{9}{{100}}\) = 3,09.
Chọn B.
Câu 5.
Phương pháp:
Biết 20% của một số là 16, muốn tìm số đó ta có thể lấy 16 chia cho 20 rồi nhân với 100 hoặc lấy 16 nhân với 100 rồi chia cho 20.
Cách giải:
20% của một số là 16.
Số đó là:
16 : 20 × 100 = 80
Chọn C.
Câu 6.
Phương pháp:
- Tính diện tích một mặt ta lấy diện tích xung quanh chia cho 4.
- Tìm độ dài cạnh dựa vào diện tích một mặt.
- Tìm thể tích hình lập phương ta lấy cạnh nhân với cạnh rồi nhân với cạnh.
Cách giải:
Diện tích một mặt của hình lập phương là:
36 : 4 = 9 (dm2)
Ta có: 3 × 3 = 9, do đó độ dài cạnh của hình lập phương đó là 3dm.
Thể tích hình lập phương đó là:
3 × 3 × 3 = 27 (dm3)
Đáp số: 27dm3.
Chọn A.
Phần 2. Tự luận
Bài 1.
Phương pháp:
Đặt tính rồi tính theo các quy tắc đã học về phép cộng, trừ, nhân, chia số thập phân.
Cách giải:
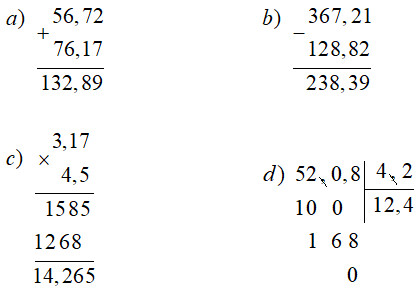
Bài 2.
Phương pháp:
Áp dụng kiến thức:
1m2 = 10000cm2 ;
1m3 = 1000dm3 hay 1dm3 = \(\dfrac{1}{{1000}}\)m3 = 0,001m3 ;
1 giờ = 60 phút hay 1 phút = \(\dfrac{1}{{60}}\)giờ ;
1kg = 1000g hay 1g = \(\dfrac{1}{{1000}}\)kg = 0,001kg.
Cách giải:
a) 0,48m2 = 4800cm2
b) 0,2kg = 200g
c) 5628dm3 = 5,628m3
d) 3 giờ 6 phút = 3,1giờ
Bài 3.
Phương pháp:
- Tính quãng đường cả hai xe đi được trong 1 giờ.
- Tính thời gian đi để gặp nhau ta lấy độ dài quãng đường AB chia cho quãng đường cả hai xe đi được trong 1 giờ.
- Tính thời điểm gặp nhau ta lấy thời gian xuất phát cộng với thời gian đi để gặp nhau.
- Khoảng cách từ A đến chỗ gặp nhau chính là quãng đường ô tô đi được trong 2 giờ. Để tìm quãng đường ta lấy vận tốc nhân với thời gian
Cách giải:
a) Sau mỗi giờ, cả hai ô tô đi được quãng đường là:
36 + 54 = 90 (km/giờ)
Thời gian đi để hai xe gặp nhau là :
180 : 90 = 2 (giờ)
Hai người gặp nhau lúc:
7 giờ 30 phút + 2 giờ = 9 giờ 30 phút
b) Chỗ gặp nhau cách A số ki-lô-mét là:
54 × 2 = 108 (km)
Đáp số: a) 9 giờ 30 phút.
b) 108km.
Bài 4.
Phương pháp:
Viết tỉ số phần trăm và số thập phân dưới dạng phân số thập phân, sau đó nhóm các phân số thích hợp lại với nhau.
Cách giải:
\(\begin{array}{l}\dfrac{{13}}{{50}} + 9\% + \dfrac{{41}}{{100}} + 0,24\\ = \dfrac{{26}}{{100}} + \dfrac{9}{{100}} + \dfrac{{41}}{{100}} + \dfrac{{24}}{{100}}\\ = \dfrac{{26 + 9 + 41 + 24}}{{100}}\\ = \dfrac{{(26 + 24) + (9 + 41)}}{{100}}\\ = \dfrac{{50 + 50}}{{100}} = \dfrac{{100}}{{100}} = 1.\end{array}\)
soanvan.me
