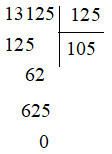Đề bài
Phần 1. Trắc nghiệm (3 điểm)
Khoanh vào chữ cái đặt trước câu trả lời đúng
Câu 1. Trong các phân số sau \(\dfrac{5}{15}; \;\dfrac{27}{36}; \; \dfrac{6}{12};\; \dfrac{99}{100};\), phân số tối giản là:
A. \(\dfrac{5}{15}\) B. \(\dfrac{27}{36}\)
C. \(\dfrac{6}{12}\) D. \(\dfrac{99}{100}\)
Câu 2. Số thích hợp điền vào chỗ chấm để 4 tấn 70kg = …..kg là:
A. 470 B. 4070
C. 4700 C. 40070
Câu 3. Điền dấu thích hợp vào chỗ chấm:
\(\dfrac{4}{5}\; ...\;\dfrac{5}{7} \)
A. > B. < C. =
Câu 4. Lớp 4A có 35 học sinh; trong đó số học sinh nam bằng \(\dfrac{4}{7}\) số học sinh cả lớp. Hỏi lớp 4A có bao nhiêu học sinh nữ?
A. 5 học sinh B. 20 học sinh
C. 15 học sinh C. 25 học sinh
Câu 5. Xe thứ nhất chở được 12 tạ gạo. Xe thứ hai chở được 1 tấn 70kg gạo. Xe thứ ba chở được 91 yến gạo. Hỏi trung bình mỗi xe chở được bao nhiêu ki-lô-gam gạo?
A. 1600kg B. 1006kg
C. 1060kg D. 700kg
Câu 6. Một hình thoi có diện tích là 250cm2, biết độ dài một đường chéo là 25cm. Tính độ dài đường chéo còn lại.
A. 10cm B. 20cm
C. 15cm D. 30cm
Phần 2. Tự luận (7 điểm)
Bài 1. Đặt tính rồi tính:
|
a) \(270973 + 72145\) |
b) \(350867 - 95709\) |
|
c) \(3076 \times 307\) |
c) \(13125:125\) |
Bài 2. Tính :
\(a)\,\,\dfrac{{13}}{{18}} - \dfrac{2}{9} + \dfrac{1}{3}\)
\(b)\,\,\dfrac{1}{2} + \dfrac{3}{4} \times \dfrac{5}{6}\)
Bài 3. Một khu vườn hình chữ nhật có chu vi \(144m\), chiều rộng bằng \(\dfrac{3}{5}\) chiều dài. Tính diện tích khu vườn đó.
Bài 4. Ba đội công nhân phải sửa đoạn đường dài 5km 460m. Đội I sửa được \(\dfrac{1}{3}\) đoạn đường, đội II sửa được số mét bằng \(\dfrac{3}{4}\) số mét đội I sửa được. Số mét còn lại đội III sửa. Hỏi mỗi đội sửa được bao nhiêu mét đường?
Lời giải chi tiết
Phần 1. Trắc nghiệm
Câu 1.
Phương pháp:
Phân số tối giản là phân số có tử số và mẫu số không cùng chia hết cho số tự nhiên nào khác 1, hay phân số tối giản là phân số không thể rút gọn được nữa.
Cách giải:
Ta có:
\(\dfrac{5}{15} = \dfrac{5:5}{15:5} = \dfrac{1}{3} ;\)
\(\dfrac{27}{36}= \dfrac{27:9}{36:9} = \dfrac{3}{4};\)
\(\dfrac{6}{12}= \dfrac{6:6}{12:6} = \dfrac{1}{2}\).
Phân số \(\dfrac{99}{100}\) có tử số và mẫu số không cùng chia hết cho số tự nhiên nào khác 1 nên là phân số tối giản.
Chọn D.
Câu 2.
Phương pháp:
Dựa vào bảng đơn vị đo khối lượng: 1 tấn = 1000kg.
Cách giải:
Ta có 1 tấn = 1000kg nên 4 tấn = 4000kg.
Do đó 4 tấn 70kg = 4 tấn + 70kg = 4000kg + 70kg = 4070kg.
Chọn B.
Câu 3.
Phương pháp:
Muốn so sánh hai phân số khác mẫu số ta có thể quy đồng mẫu số hai phân số rồi so sánh hai phân số đó.
Cách giải:
Ta có:
\(\dfrac{4}{5} = \dfrac{{4 \times 7}}{{5 \times 7}} = \dfrac{{28}}{{35}};\,\) \(\dfrac{5}{7} = \dfrac{{5 \times 5}}{{7 \times 5}} = \dfrac{{25}}{{35}}.\)
Mà: \(\dfrac{{28}}{{35}} > \dfrac{{25}}{{35}}\) (Vì 28 > 25).
Vậy: \(\dfrac{4}{5} > \dfrac{5}{7}.\)
Chọn A.
Câu 4.
Phương pháp:
- Tìm số học sinh nam ta lấy số học sinh cả lớp nhân với \(\dfrac{4}{7}\) .
- Tìm số học sinh nữ = số học sinh cả lớp – số học sinh nam.
Cách giải:
Lớp 4A có số học sinh nam là:
35 × \(\dfrac{4}{7}\) = 20 (học sinh)
Lớp 4A có số học sinh nữ là:
35 – 20 = 15(học sinh)
Đáp số: 15 học sinh
Chọn C.
Câu 5.
Phương pháp:
- Đổi các số đo khối lượng sang đơn vị ki-lô-gam, lưu ý rằng: 1 tấn = 1000kg; 1 tạ = 100kg; 1 yến = 10kg.
- Số gạo trung bình mỗi xe chở được = Tổng số gạo ba xe chở được : 3.
Cách giải:
Đổi: 12 tạ = 1200kg
1 tấn 70kg = 1070kg
91 yến = 910kg
Trung bình mỗi xe chở được số ki-lô-gam gạo là:
(1200 + 1070 + 910) : 3 = 1060 (kg)
Đáp số: 1060kg.
Chọn C. 1060kg
Câu 6.
Phương pháp:
Muốn tìm độ dài đường chéo còn lại ta lấy 2 lần diện tích chia cho độ dài đường chéo đã biết.
Cách giải:
Độ dài đường chéo còn lại là:
250 × 2 : 25 = 20 (cm)
Đáp số: 20cm.
Chọn B.
Phần 2. Tự luận
Bài 1.
Phương pháp:
Đặt tính rồi tính theo các quy tắc đã học.
Cách giải:
|
a) \(\dfrac{{ + \begin{array}{*{20}{r}}{270973}\\{72145}\end{array}}}{{\,\,\,\,343118}}\) |
b) \(\dfrac{{ - \begin{array}{*{20}{r}}{350867}\\{95709}\end{array}}}{{\,\,255158}}\) |
|
c) \(\dfrac{{ \times \begin{array}{*{20}{r}}{\,\,\,\,\,3076}\\{307}\end{array}}}{{\,\,\,\,944332}}\) |
d) |
Bài 2.
Phương pháp:
- Biểu thức chỉ có phép tính cộng, trừ hoặc chỉ có phép tính nhân, chia thì thực hiện theo thứ tự từ trái sang phải.
- Biểu thức có các phép tính cộng, trừ, nhân, chia thì thực hiện phép nhân, chia trước; thực hiện phép cộng, trừ sau.
Cách giải:
| \(\begin{array}{l}a){\mkern 1mu} {\mkern 1mu} \dfrac{{13}}{{18}} - \dfrac{2}{9} + \dfrac{1}{3}\\\,\,\, = \dfrac{{13}}{{18}} - \dfrac{4}{{18}} + \dfrac{1}{3}\\\,\,\, = \dfrac{9}{{18}} + \dfrac{1}{3}\\\,\,\, = \dfrac{1}{2} + \dfrac{1}{3}\\\,\,\, = \dfrac{3}{6} + \dfrac{2}{6}\\\,\,\, = \dfrac{5}{6}\end{array}\) |
\(\begin{array}{l}b){\mkern 1mu} {\mkern 1mu} \dfrac{1}{2} + \dfrac{3}{4} \times \dfrac{5}{6}\\\,\,\,\, = \dfrac{1}{2} + \dfrac{{15}}{{24}}\\\,\,\,\, = \dfrac{1}{2} + \dfrac{5}{8}\\\,\,\,\, = \dfrac{4}{8} + \dfrac{5}{8}\\\,\,\,\, = \dfrac{9}{8}\end{array}\) |
Bài 3.
Phương pháp:
- Tìm chiều dài, chiều rộng theo bài toán tìm hai số khi biết tổng và tỉ số của hai số đó.
- Diện tích = chiều dài \(\times \) chiều rộng.
Cách giải:
Nửa chu vi khu vườn hình chữ nhật là:
144:2 = 72 (m)
Ta có sơ đồ:
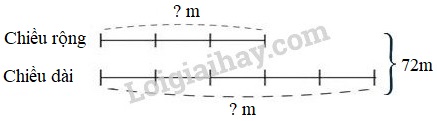
Theo sơ đồ, tổng số phần bằng nhau là:
5 + 3 = 8 (phần)
Chiều rộng hình khu vườn hình chữ nhật là:
72 : 8 × 3 = 27 (m)
Chiều dài khu vườn hình chữ nhật là:
72 – 27 = 45 (m)
Diện tích khu vườn hình chữ nhật là:
45 × 27 = 1215 (m2)
Đáp số: 1215m2.
Bài 4.
Phương pháp:
- Đổi: 5km 460m = 5460m.
- Tính số mét đường đội I sửa = độ dài đoạn đường \(\times \,\dfrac{1}{3}\).
- Tính số mét đường đội II sửa = số mét đường đội I sửa \(\times \,\dfrac{3}{4}\).
- Tính số mét đường đội III sửa = độ dài đoạn đường \(-\) số mét đường đội I sửa \(-\) số mét đường đội II sửa.
Cách giải:
Đổi: 5km 460m = 5460m.
Đội I sửa được số mét đường là:
5460 × \(\dfrac{1}{3}\) = 1820 (m)
Đội II sửa được số mét đường là:
1820 × \(\dfrac{3}{4}\) = 1365 (m)
Đội III sửa được số mét đường là:
5460 – 1820 – 1365 = 2275 (m)
Đáp số: Đội I: 1820m;
Đội II: 1365m;
Đội III: 2275m.
soanvan.me