Đề bài
Câu 1. Viết phân số chỉ phần tô đậm trong mỗi hình vẽ sau:
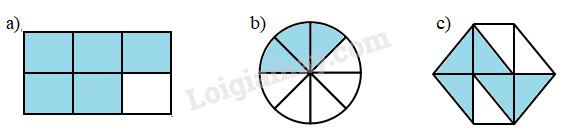
Câu 2. Đúng ghi Đ, sai ghi S vào ô trống:
|
a) Phân số \(\dfrac{3}{4}\) đọc là: Ba phần bốn |
|
|
b) Phân số \(\dfrac{2}{5}\) đọc là: Hai phần năm |
|
|
c) Phân số \(\dfrac{1}{3}\) đọc là: Ba phần một |
|
|
d) Phân số \(\dfrac{1}{2}\) đọc là: Một phần hai |
|
Câu 3. Khoanh vào chữ đặt trước câu trả lời đúng:
A) Phân số \(\dfrac{5}{6}\) có tử số là 5, mẫu số là 6.
B) Phần số \(\dfrac{5}{9}\) có tử số là 9, mẫu số là 5.
C) Phân số \(\dfrac{4}{5}\) có tử số là 4, mẫu số là 5.
Câu 4. Đúng ghi Đ, sai ghi S vào ô trống:
|
a) \(\dfrac{{12}}{{14}} = \dfrac{6}{7}\) |
|
|
b) \(\dfrac{3}{5} = \dfrac{6}{{10}}\) |
|
|
c) \(\dfrac{{24}}{{18}} = \dfrac{{12}}{{10}}\) |
|
|
d) \(\dfrac{{32}}{{40}} = \dfrac{4}{5}\) |
|
Câu 5. Khoanh vào chữ đặt trước câu trả lời đúng:
A) \(\dfrac{{10}}{{11}} < 1\) B) \(\dfrac{{100}}{{99}} > 1\)
C) \(\dfrac{{14}}{{15}} < 1\) D) \(\dfrac{{20}}{{18}} < 1\)
Câu 6. Viết số thích hợp vào chỗ chấm:
a) \(\dfrac{3}{5} = \dfrac{{3 \times 2}}{{5 \times \ldots }} = \dfrac{ \ldots }{ \ldots }\)
b) \(\dfrac{4}{3} = \dfrac{{4 \times 3}}{{3 \times \ldots }} = \dfrac{ \ldots }{ \ldots }\)
c) \(\dfrac{{12}}{{24}} = \dfrac{{12: \ldots }}{{24:12}} = \dfrac{ \ldots }{ \ldots }\)
d) \(\dfrac{1}{4} = \dfrac{{1 \times \ldots }}{{4 \times 3}} = \dfrac{ \ldots }{ \ldots }\)
Câu 7. Viết thương của mỗi phép chia sau (theo mẫu):
\(3:5 = \dfrac{3}{5}\): Ba phần năm
a) \(7:11 = \ldots \)
b) \(9:14 = \ldots \)
c) \(12:17 = \ldots \)
d) \(21:50 = \ldots \)
Câu 8. Viết vào chỗ chấm (theo mẫu):
\(\dfrac{4}{5}\)m: Bốn phần năm mét
a) \(\dfrac{6}{7}\)kg: ……
b) \(\dfrac{{15}}{{23}}\) tạ: ……
c) \(\dfrac{7}{8}\)km: …….
d) \(\dfrac{{11}}{{17}}\) km2: ……
Câu 9. Viết 5 phân số mà mỗi phân số đều nhỏ hơn 1 và có chung mẫu là 6.
Câu 10: Khi nhân cả tử số và mẫu số của phân số với 7 ta được phân số \(\dfrac{{21}}{{49}}\). Tìm phân số đó.
Lời giải chi tiết
Câu 1.
Phương pháp:
Phân số chỉ phần tô đậm của mỗi hinh có tử số là số phần được tô màu, mẫu số là tổng số phần bằng nhau của hình đó.
Cách giải:
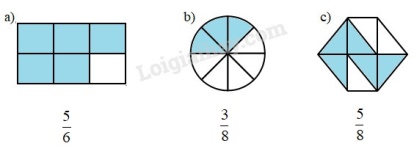
Câu 2.
Phương pháp:
Khi đọc phân số ta đọc tử số trước, đọc "phần" rồi sau đó đọc mẫu số.
Cách giải:
|
a) Phân số \(\dfrac{3}{4}\) đọc là: Ba phần bốn |
Đ |
|
b) Phân số \(\dfrac{2}{5}\) đọc là: Hai phần năm |
Đ |
|
c) Phân số \(\dfrac{1}{3}\) đọc là: Ba phần một |
S |
|
d) Phân số \(\dfrac{1}{2}\) đọc là: Một phần hai |
Đ |
Câu 3.
Phương pháp:
Mỗi phân số có tử số và mẫu số. Tử số là số tự nhiên viết trên gạch ngang. Mẫu số là số tự nhiên khác 0 viết dưới gạch ngang.
Cách giải:
Phân số \(\dfrac{5}{6}\) có tử số là 5, mẫu số là 6.
Phần số \(\dfrac{5}{9}\) có tử số là 5, mẫu số là 9.
Phân số \(\dfrac{4}{5}\) có tử số là 4, mẫu số là 5.
Vậy câu đúng là A và C.
Chọn A, C.
Câu 4.
Phương pháp:
Áp dụng tính chất cơ bản của phân số:
- Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
- Nếu cả tử số và mẫu số của một phân số cùng chia hết cho một số tự nhiên khác 0 thì sau khi chia ta được một phân số bằng phân số đã cho.
Cách giải:
Ta có:
a) \(\dfrac{{12}}{{14}} = \dfrac{{12:2}}{{14:2}}= \dfrac{6}{7}\)
b) \(\dfrac{3}{5}= \dfrac{3\times 2}{5 \times 2}= \dfrac{6}{{10}}\)
c) \(\dfrac{{24}}{{18}} = \dfrac{{24:6}}{{18:6}}= \dfrac{4}{3} ; \dfrac{{12}}{{10}}= \dfrac{{12:2}}{{10:2}}=\dfrac{6}{5}\)
d) \(\dfrac{{32}}{{40}} =\dfrac{{32:8}}{{40:8}}= \dfrac{4}{5}\)
Vậy ta có bảng kết quả như sau:
|
a) \(\dfrac{{12}}{{14}} = \dfrac{6}{7}\) |
Đ |
|
b) \(\dfrac{3}{5} = \dfrac{6}{{10}}\) |
Đ |
|
c) \(\dfrac{{24}}{{18}} = \dfrac{{12}}{{10}}\) |
S |
|
d) \(\dfrac{{32}}{{40}} = \dfrac{4}{5}\) |
Đ |
Câu 5.
Phương pháp:
- Phân số có tử số nhỏ hơn mẫu số thì phân số đó nhỏ hơn 1.
- Phân số có tử số lớn hơn mẫu số thì phân số đó lớn hơn 1.
Cách giải:
Ta có:
\(\dfrac{{10}}{{11}} < 1\) \(\dfrac{{100}}{{99}} > 1\)
\(\dfrac{{14}}{{15}} < 1\) \(\dfrac{{20}}{{18}} >1\)
Vậy câu trả lời đúng là A; B; C.
Chọn A; B; C
Câu 6.
Phương pháp:
Áp dụng tính chất cơ bản của phân số:
- Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
- Nếu cả tử số và mẫu số của một phân số cùng chia hết cho một số tự nhiên khác 0 thì sau khi chia ta được một phân số bằng phân số đã cho.
Cách giải:
a) \(\dfrac{3}{5} = \dfrac{{3 \times 2}}{{5 \times 2}} = \dfrac{6}{{10}}\)
b) \(\dfrac{4}{3} = \dfrac{{4 \times 3}}{{3 \times 3}} = \dfrac{{12}}{9}\)
c) \(\dfrac{{12}}{{24}} = \dfrac{{12:12}}{{24:12}} = \dfrac{1}{2}\)
d) \(\dfrac{1}{4} = \dfrac{{1 \times 3}}{{4 \times 3}} = \dfrac{3}{{12}}\)
Câu 7.
Phương pháp:
Thương của phép chia số tự nhiên cho số tự nhiên (khác 0) có thể viết thành một phân số, tử số là số bị chia và mẫu số là số chia.
Cách giải:
a) \(7:11 = \dfrac{7}{{11}}\) b) \(9:14 = \dfrac{9}{{14}}\)
c) \(12:17 = \dfrac{{12}}{{17}}\) d) \(21:50 = \dfrac{{21}}{{50}}\)
Câu 8.
Phương pháp:
Khi đọc phân số ta đọc tử số trước, đọc "phần" rồi sau đó đọc mẫu số. Nếu có đơn vị đo thì ta đọc thêm tên đơn vị đo.
Cách giải:
a) \(\dfrac{6}{7}\)kg: Sáu phần bảy ki-lô-gam.
b) \(\dfrac{{15}}{{23}}\) tạ: Mười lăm phần hai mươi ba tạ.
c) \(\dfrac{7}{8}\)km: Bảy phần tám ki-lô-mét.
d) \(\dfrac{{11}}{{17}}\) km2: Mười một phần mười bảy ki-lô-mét vuông.
Câu 9.
Phương pháp:
Phân số có tử số nhỏ hơn mẫu số thì phân số đó nhỏ hơn 1.
Cách giải:
5 phân số mà mỗi phân số đều nhỏ hơn 1 và có chung mẫu là 6 là:
\(\dfrac{5}{6}\,;\,\,\dfrac{4}{6}\,;\,\,\dfrac{3}{6}\,;\,\,\dfrac{2}{6}\,;\,\,\dfrac{1}{6}\).
Câu 10:
Phương pháp:
Áp dụng tính chất cơ bản của phân số:
- Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
- Nếu cả tử số và mẫu số của một phân số cùng chia hết cho một số tự nhiên khác 0 thì sau khi chia ta được một phân số bằng phân số đã cho.
Cách giải:
Gọi phân số cần tìm là \(\dfrac{a}{b}\).
Theo đề bài ta có:
\(\begin{array}{l}\dfrac{{a \times 7}}{{b \times 7}} = \dfrac{{21}}{{49}}\\ \Rightarrow a \times 7 =21 \;; \quad b \times 7=49 \\ \Rightarrow a =3\;; \quad b=7 \\ \Rightarrow \dfrac{a}{b} = \dfrac{3}{7}\end{array}\).
Vậy phân số cần tìm là \(\dfrac{3}{7}\).
soanvan.me
