Đề bài
Chu vi hình chữ nhật \(ABCD\) là \(20cm\). Hãy tìm giá trị nhỏ nhất của độ dài đường chéo \(AC\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+) Áp dụng định lý Py-ta-go.
+) Đánh giá \(A^2+m \ge m\), dấu "=" xảy ra khi \(A=0.\)
Lời giải chi tiết
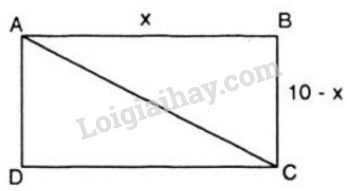
Gọi \(x\) (\(cm\)) là độ dài cạnh \(AB\)
Vì nửa chu vi hình chữ nhật đã cho là: \(20:2=10 \, cm\) nên \(AB+BC=10cm\) suy ra \(BC=10 – x \, (cm).\)
Áp dụng định lí Py-ta-go trong tam giác vuông \(ABC\), ta có:
\(\eqalign{
& A{C^2} = A{B^2} + B{C^2} \cr
& = {x^2} + {\left( {10 - x} \right)^2} \cr
& = 2\left( {{x^2} - 10{\rm{x}} + 50} \right) \cr
& = 2\left[ {{{\left( {x - 5} \right)}^2} + 25} \right] \cr}\)
Vì \((x-5)^2 \geq 0, \forall x \in \mathbb{R}\)
\(\Rightarrow A{C^2} = 2{\left( {x - 5} \right)^2} + 50 \ge 50, \forall x \in \mathbb{R}\)
Dấu "=" xảy ra khi : \(x – 5 = 0 ⇔ x = 5\)
Vậy giá trị nhỏ nhất của đường chéo AC là \(\sqrt{50} = 5\sqrt2\) (\(cm\))
