Đề bài
Cho tam giác nhọn \(ABC\) nội tiếp đường tròn \((O)\). Các cung nhỏ \(AB, BC, CA\) có số đo lần lượt là \(x + 75^0, 2x + 25^0, 3x - 22^0\). Một góc của tam giác \(ABC\) có số đo là:
(A) \(57^05\) ; (B) \(59^0\) ; (C) \(61^0\) ; (D) \(60^0\)
Hãy chọn câu trả lời đúng.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+) Số đo cả đường tròn bằng \(360^0.\)
+) Góc nội tiếp có số đo bằng nửa số đo cung bị chắn.
Lời giải chi tiết
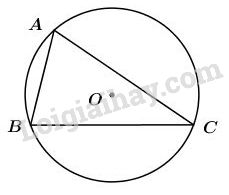
Vì các cung \(AB, BC, CA\) tạo thành đường tròn, do đó:
\((x + {75^0}) + (2x + {25^0}) + (3x - {22^0}) = {360^0}\)
\(\Leftrightarrow 6x + {78^0} = {360^0} \Leftrightarrow 6x = {282^0} \Leftrightarrow x = {47^0}\)
Vậy \(sđ\overparen{AB}=x + {75^0} = {47^0} + {75^0} = {122^0}\)
\(sđ\overparen{BC}=2x + {25^0} = {2. 47^0} + {25^0} = {119^0}\)
\(sđ\overparen{AB}=3x - {22^0} = {3.47^0} - {22^0} = {119^0}\)
Xét đường tròn \(O\) có góc A, B, C lần lượt là góc nội tiếp chắn \(\overparen{BC}; \overparen{AC}; \overparen{AB}\)
\(\Rightarrow \widehat A = {{{sđ\overparen{BC}}} \over 2}= {{{{119}^0}} \over 2} = 59,{5^0}\)
\(\Rightarrow \widehat B = {{{sđ\overparen{AC}}} \over 2}={{{{119}^0}} \over 2} = 59,{5^0}\)
\(\Rightarrow \widehat C = {{{sđ\overparen{AB}}} \over 2}= {{{{122}^0}} \over 2} = {61^0}\)
Chọn đáp án C
