Đề bài
Cho tam giác đều ABC nội tiếp đường tròn (O). Kẻ các đường kính AA’, BB’, CC’. Tính số đo:
a) Các góc ở tâm \(\widehat {AOB},\widehat {BOA'},\widehat {B'OC'},\widehat {COC'}.\)
b) Các cung ABC’, ABC, ACC’, BCB’.
Phương pháp giải - Xem chi tiết
a) +) Sử dụng tính chất: Tam giác đều có tâm đường tròn ngoại tiếp đồng thời là giao điểm các đường phân giác, tính \(\widehat {AOB}\).
+) Sử dụng tổng hai góc kề bù tính \(\widehat {BOA'}\).
+) Tương tự tính \(\widehat {AOB'} = \widehat {AOC'}\), từ đó tính \(\widehat {B'OC'}\).
+) CC’ là đường kính, tính \(\widehat {COC'}\).
b) Số đo góc ở tâm bằng số đo cung bị chắn.
Lời giải chi tiết
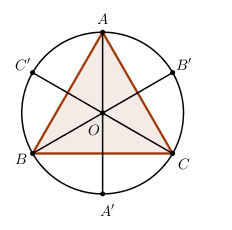
Do tam giác ABC đều nên O là tâm đường tròn ngoại tiếp đồng thời là giao điểm của các đường phân giác.
\( \Rightarrow AA'\) là tia phân giác của \(\widehat {BAC}\) và \(BB'\) là tia phân giác của \(\widehat {ABC}\).
\( \Rightarrow \widehat {OAB} = \dfrac{1}{2}{.60^0} = {30^0};\,\,\widehat {OBA} = \dfrac{1}{2}{.60^0} = {30^0}\).
+) Xét tam giác OAB có: \(\widehat {OAB} + \widehat {OBA} + \widehat {AOB} = {180^0}\) (tổng 3 góc trong một tam giác).
\( \Rightarrow {30^0} + {30^0} + \widehat {AOB} = {180^0}\) \( \Leftrightarrow \widehat {AOB} = {120^0}\).
+) Ta có: \(\widehat {AOB} + \widehat {BOA'} = {180^0}\) (hai góc kề bù) \( \Rightarrow \widehat {BOA'} = {180^0} - \widehat {AOB} = {180^0} - {120^0} = {60^0}\).
+) Chứng minh tương tự ta có \(\widehat {AOB'} = \widehat {AOC'} = {60^0} \) \(\Rightarrow \widehat {B'OC'} = \widehat {AOB'} + \widehat {AOC'} = {60^0} + {60^0} = {120^0}\).
+) Vì CC’ là đường kính của đường tròn (O) \( \Rightarrow \widehat {COC'} = {180^0}\).
b) Ta có .
Chứng minh tương tự ta có \(\widehat {AOC} = \widehat {BOC} = {120^0}\)
\( \Rightarrow sd\,cung\,ABC = {360^0} - sd\,cung\,AOC\)\(\, = {360^0} - \widehat {AOC} = {360^0} - {240^0} = {120^0}\).
\(sd\,cung\,ACC' = sd\,cung\,ABC' = {300^0}\).
\(sd\,cung\,BCB' = \widehat {BOB'} = {180^0}\).
soanvan.me
