Đề bài
Cho tam giác \(ABC\) có ba góc nhọn và \(H\) là trực tâm. Tìm ảnh của tam giác \(ABC\) qua phép vị tự tâm \(H\), tỉ số \( \frac{1}{2}.\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+) Tìm ảnh của từng đỉnh. Ảnh của tam giác là tam giác tạo bởi ba điểm ảnh đó.
+) \({V_{(H,\frac 1 2)}}(M) = M'\Leftrightarrow \overrightarrow {HM'} = \frac 1 2.\overrightarrow {HM} \)
Lời giải chi tiết
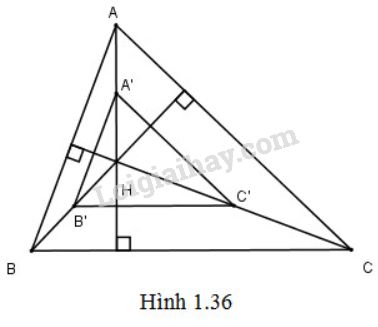
Gọi \(A',B',C'\) lần lượt là ảnh của \(A,B,C\) qua \({V_{\left( {H,\dfrac{1}{2}} \right)}}\) ta có:
+) \(A' = {V_{\left( {H,\dfrac{1}{2}} \right)}}\left( A \right) \Rightarrow \overrightarrow {HA'} = \dfrac{1}{2}\overrightarrow {HA} \)\( \Rightarrow A'\) là trung điểm của \(AH\).
+) \(B' = {V_{\left( {H,\dfrac{1}{2}} \right)}}\left( B \right) \Rightarrow \overrightarrow {HB'} = \dfrac{1}{2}\overrightarrow {HB} \)\( \Rightarrow B'\) là trung điểm của \(BH\).
+) \(C' = {V_{\left( {H,\dfrac{1}{2}} \right)}}\left( C \right) \Rightarrow \overrightarrow {HC'} = \dfrac{1}{2}\overrightarrow {HC} \)\( \Rightarrow C'\) là trung điểm của \(CH\).
Vậy \({V_{\left( {H,\frac{1}{2}} \right)}}(\Delta ABC) = A'B'C'\), trong đó \(A', B', C'\) lần lượt là trung điểm của \(HA, HB, HC\).
soanvan.me
