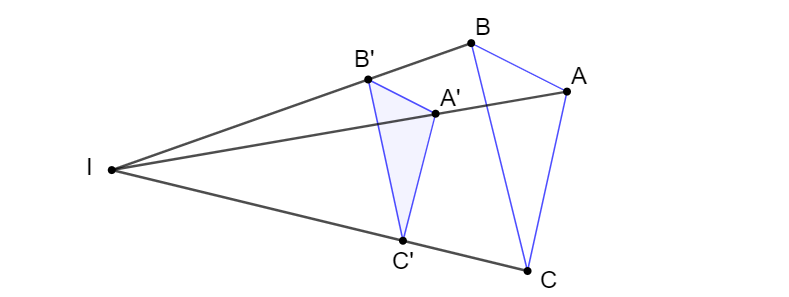
1. Định nghĩa
Cho điểm \(O\) và số \(k \ne 0\). Phép biến hình biến mỗi điểm \(M\) thành điểm \(M'\) sao cho \(\overrightarrow{OM'} = k\) \(\overrightarrow{OM}\), được gọi là phép vị tự tâm \(O\), tỉ số \(k\)
Phép vị tự tâm \(O\), tỉ số \(k\) và thường được kí hiệu là \({V_{(O,k)}}\)
Nhận xét
- Phép vị tự biến tâm vị tự thành chính nó
- Khi \(k=1\), phép vị tự là phép đồng nhất
- Khi \(k = -1\), phép vị tự là phép đối xứng qua tâm vị tự
- \(M'\) = \({V_{(O,k)}}^{} (M)\) \( ⇔ M =\) \({V_{(O,\frac{1}{k})}} (M')\)
2. Tính chất
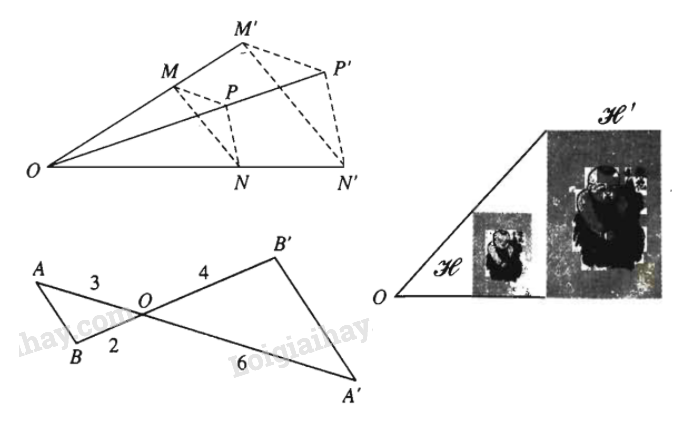
- Nếu phép vị tự tâm \(O\) tỉ số \(k\) biến hai điểm \(M, N\) tùy ý theo thứ tự thành \(M', N'\) thì \(\overrightarrow{M'N'}\) =\( k \overrightarrow{MN}\) và \(M'N' = |k| MN\)
- Phép vị tự tỉ số \(k\) có các tính chất:
a) Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các điểm ấy
b) Biến đường thẳng thành đường thẳng song song hoặc trùng với nó, biến tia thành tia, biến đoạn thẳng có độ dài bằng \(a\) thành đoạn thẳng có độ dài bằng \(|k| a\)
c) Biến tam giác thành tam giác đồng dạng với tỉ số đồng dạng là \(|k|\), biến góc thành góc bằng nó.
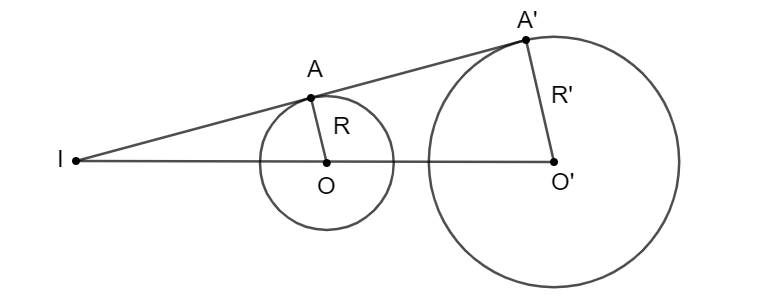
d) Biến đường tròn bán kính \(R\) thành đường tròn bán kính \(|k|R\).
3. Tâm vị tự của hai đường tròn
Định lí: Với hai đường tròn bất kì, luôn có một phép vị tự biến đường tròn này thành đường tròn kia.
Cách tìm tâm vi tự:
+ TH1: hai tâm trùng nhau
+ TH2: hai tâm khác nhau
+ Th3: hai tâm khác nhau, bán kính bằng nhau
4. Biểu thức tọa độ của phép vị tự
Cho điểm \(M\left( {{x_0};{y_0}} \right)\).
Phép vị tự tâm \(O\left( {a;b} \right)\), tỉ số \(k\) biến điểm \(M\) thành \(M'\) có tọa độ \(\left( {x';y'} \right)\) thỏa mãn:
\(\left\{ \begin{array}{l}x' - a = k\left( {{x_0} - a} \right)\\y' - b = k\left( {{y_0} - b} \right)\end{array} \right.\)
soanvan.me