Đề bài
Cho đường tròn (O) có các dây AB và CD bằng nhau, các tia AB và CD cắt nhau tại điểm E nằm bên ngoài đường tròn. Gọi H và K theo thứ tự là trung điểm của AB và CD. Chứng minh rằng:
a) EH = EK
b) EA = EC.
Phương pháp giải - Xem chi tiết
a) Dùng phương pháp hai tam giác bằng nhau.
b) Chứng minh \(HA = KC\) và kết hợp với câu a.
Lời giải chi tiết
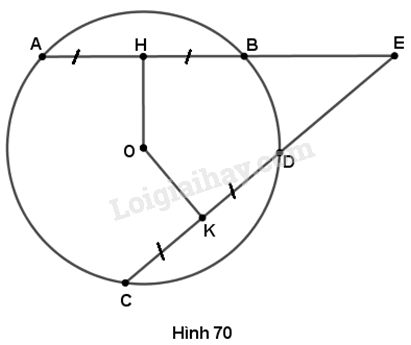
a) Ta có \(HA = HB,KC = KD\) nên \(OH \bot AB,OK \bot CD.\)
Ta có \(AB = CD\left( {gt} \right)\) nên \(OH = OK\) (vì hai dây bằng nhau thì cách đều tâm).
Các tam giác vuông \(OEH\) và \(OEK\) có \(\widehat H = \widehat K = {90^o},OE\) là cạnh chung, \(OH = OK\) (chứng minh trên).
Do đó, \(\Delta OEH = \Delta OEK\) (trường hợp cạnh huyền – cạnh góc vuông ). Suy ra
\(EH = EK{\rm{ }}\left( 1 \right)\)
b) Ta có \(HA = \dfrac{{AB}}{2},KC = \dfrac{{CD}}{2},\) mà \(AB = CD\) nên
\(HA = HC{\rm{ }}\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(EH + HA = EK + KC\) tức là \(EA = EC.\)
soanvan.me
