Đề bài
Cho hình 72 trong đó hai đường tròn có cùng tâm O. Cho biết AB > CD. Hãy so sánh các độ dài:
a) OH và OK
b) ME và MF
c) MH và MK
Phương pháp giải - Xem chi tiết
Dùng định lí dây nào lớn hơn thì gần tâm hơn và ngược lại.
Lời giải chi tiết
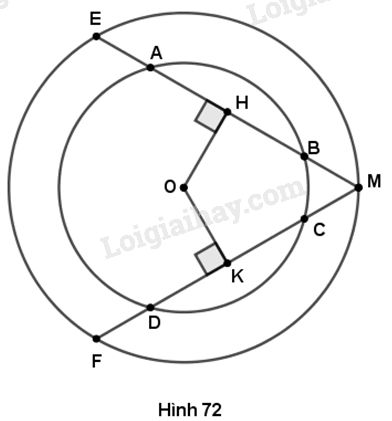
a) Xét đường tròn nhỏ, \(OH\) và \(OK\) là khoảng cách từ tâm đến các dây \(AB\) và CD.
Do \(AB > CD\) (giả thiết) nên \(OH < OK\)(vì dây \(AB\) lớn hơn thì gần tâm hơn).
b) Xét đường tròn lớn, khoảng cách từ tâm đến các dây \(ME\) và MF là \(OH\) và OK.
Do \(OH < OK\) (câu a) nên \(ME > MF\) (vì dây \(ME\) gần tâm hơn thì lớn hơn).
c) Xét đường tròn lớn, do \(OH \bot ME\) nên \(MH = HE = \dfrac{1}{2}ME.\) ( đường kính vuông góc với dây thì đi qua trung điểm của dây)
Tương tự, do \(OK \bot MF\) nên \(KM = KF = \dfrac{1}{2}MF.\)
Ta lại có \(ME > MF\) (câu b) nên \(MH > MK.\)
soanvan.me
