Đề bài
Cho đường tròn tâm (O), điểm A nằm bên ngoài vòng tròn. Vẽ dây BC vuông góc với OA tại A. Vẽ dây EF bất kì đi qua A và không vuông góc với OA. So sánh độ dài hai dây BC và EF.
Phương pháp giải - Xem chi tiết
- Dùng kiến thức về mối quan hệ giữa cạnh huyền và cạnh góc vuông trong một tam giác vuông và định lí “trong một đường tròn dây nào lớn hơn thì gần tâm hơn”.
Lời giải chi tiết
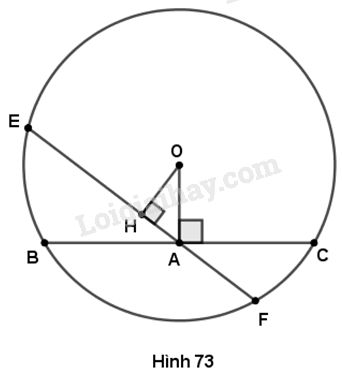
Kẻ \(OH \bot EF.\) Ta có khoảng cách từ tâm \(O\) đến dây \(BC\) là \(OA\), khoảng cách từ tâm \(O\) đến dây \(EF\) là \(OH\).
Xét tam giác \(OHA\) vuông tại \(H\) ta có :
\(OA > OH\) (vì trong tam giác vuông, cạnh huyền lớn hơn cạnh góc vuông).
Do \(OA > OH\) nên \(BC < EF\) (vì dây \(EF\) gần tâm hơn thì lớn hơn).
soanvan.me
