Đề bài
Trên dây cung \(AB\) của một đường tròn \(O,\) lấy hai điểm \(C\) và \(D\) chia dây này thành ba đoạn thẳng bằng nhau \(AC = CD = DB.\) Các bán kính qua \(C\) và \(D\) cắt cung nhỏ \(AB\) lần lượt tại \(E\) và \(F.\) Chứng minh rằng:
\(a)\) \(\overparen{AE}\) = \(\overparen{FB};\)
\(b)\) \(\overparen{AE}\) < \(\overparen{EF}.\)
Phương pháp giải - Xem chi tiết
Ta sử dụng kiến thức:
+) Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.
+) Hai tam giác có hai cạnh bằng nhau từng đôi một, cạnh thứ ba không bằng nhau, đối diện cạnh lớn hơn là góc lớn hơn.
Lời giải chi tiết
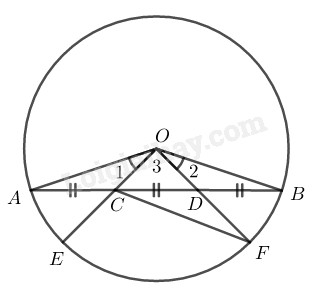
\(a)\) \(∆OAB\) cân tại \(O\) (vì \(OA = OB\) = bán kính)
\( \Rightarrow \widehat A = \widehat B\)
Xét \(∆OAC\) và \(∆OBD:\)
\(OA = OB\) (bán kính)
\(\widehat A = \widehat B\) (chứng minh trên)
\(AC = BD\;\; (gt)\)
Suy ra: \(∆OAC = ∆OBD\;\; (c.g.c)\)
\( \Rightarrow \widehat {{O_1}} = \widehat {{O_2}}\) \( (1)\)
\(sđ \overparen{AE} = \widehat {{O_1}}\) \((2)\)
\(sđ \overparen{BF} = \widehat {{O_2}}\) \((3)\)
Từ \((1),\) \((2)\) và \((3)\) suy ra: \(\overparen{AE} = \overparen{BF}\)
\(b)\) \(∆OAC = ∆BOD\) (chứng minh trên)
\( \Rightarrow OC = OD\)
\( \Rightarrow \Delta OCD\) cân tại \(O\) nên \(\widehat {ODC} < {90^0}\) mà \(\widehat {ODC}+\widehat {CDF} = {180^0}\) (hai góc kề bù)
Suy ra: \(\widehat {CDF} > {90^0}\)
Trong \(∆CDF\) ta có: \(\widehat {CDF} > {90^0} \Rightarrow CF > CD\) nên \(AC < CF\)
Xét \(∆OAC\) và \(∆OCF:\)
\(OA = OF\) (= bán kính)
\(OC\) cạnh chung
\(AC < CF\)
Suy ra: \(\widehat {{O_1}} < \widehat {{O_3}}\) (hai tam giác có \(2\) cạnh bằng nhau từng đôi một, cạnh thứ \(3\) không bằng nhau thì đối diện cạnh lớn hơn là góc lớn hơn).
\(sđ \overparen{AE} =\widehat {{O_1}}\)
\(sđ \overparen{EF} = \widehat {{O_3}}\)
Suy ra: \(\overparen{AE} < \overparen{EF}\).
soanvan.me
