Đề bài
Cho đường tròn \((O).\) Gọi \(I\) là điểm chính giữa dây cung \(AB\) (Không phải là cung nửa đường tròn) và \(H\) là trung điểm của dây \(AB.\) Chứng minh rằng đường thẳng \(IH\) đi qua tâm \(O\) của đường tròn.
Phương pháp giải - Xem chi tiết
Ta sử dụng kiến thức:
+) Với hai cung nhỏ trong một đường tròn, hai cung bằng nhau căng hai dây bằng nhau.
+) Tính chất đường trung trực: Điểm cách đều hai đầu mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.
Lời giải chi tiết
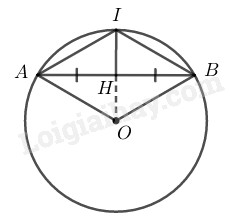
Ta có: \(\overparen{IA}= \overparen{IB}\) \((gt)\)
\( \Rightarrow IA = IB\) (\(2\) cung bằng nhau căng \(2\) dây bằng nhau)
\( \Rightarrow I\) nằm trên đường trung trực của \(AB\)
\(OA = OB\) (bán kính \((O)\))
\( \Rightarrow O\) nằm trên đường trung trực của \(AB\)
Suy ra: \(OI\) là đường trung trực của \(AB\)
\(H\) là trung điểm của \(AB,\) do đó \(OI\) đi qua trung điểm \(H\)
Vậy \(3\) điểm \(I, H, O\) thẳng hàng.
soanvan.me
