Đề bài
Cho đường tròn tâm \(O.\) Trên nửa đường tròn bán kính \(AB\) lấy hai điểm \(C, D.\)Từ \(C\) kẻ CH vuông góc với \( AB,\) nó cắt đường tròn tại điểm thứ hai là \(E.\)Từ \(A\) kẻ AK vuông góc với \(DC,\) nó cắt đường tròn tại điểm thứ hai là \(F.\) Chứng minh rằng:
\(a)\) Hai cung nhỏ \(CF\) và \(DB\) bằng nhau.
\(b)\) Hai cung nhỏ \(BF\) và \(DE\) bằng nhau.
\(c)\) \(DE = BF.\)
Phương pháp giải - Xem chi tiết
Ta sử dụng kiến thức:
+) Tam giác nội tiếp đường tròn có một cạnh là đường kính thì tam giác đó là tam giác vuông.
+) Với hai cung nhỏ ttrong một đường tròn, hai cung chắn giữa hai đường thẳng song song thì bằng nhau.
+) Nếu \(C\) là một điểm trên cung \(AB\) thì: \(sđ \overparen{AB}=sđ \overparen{AC}+sđ \overparen{CB}.\)
+) Với hai cung nhỏ trong một đường tròn, hai cung bằng nhau căng hai dây bằng nhau.
Lời giải chi tiết
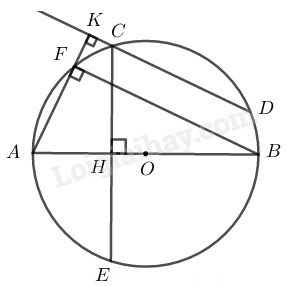
\(a)\) \(∆ AFB\) nội tiếp trong \((O)\) có
\(AB\) là đường kính nên \(∆ AFB\) vuông tại \(F.\)
\( \Rightarrow BF \bot AK\)
\(AK \bot CD\) \((gt)\)
Suy ra: \(BF // CD\)
\( \Rightarrow \) \(\overparen{BD}= \overparen{CF}\) (hai cung chắn giữa hai dây song song thì bằng nhau)
\(b)\) Đường kính \(AB \bot CE\) tại điểm \(H\) nên H là trung điểm của CE
Suy ra \(C\) và \(E\) đối xứng qua trục \(AB.\)
\( \Rightarrow BC=BE\) nên \(\overparen{BC} = \overparen{BE}\)
\(\overparen{CF} = \overparen{BD}\) (chứng minh trên)
Suy ra: \(\overparen{BC} + \overparen{CF}= \overparen{BE} + \overparen{BD}\)
Hay \(\overparen{BF} = \overparen{DE}\)
\(c)\) \(\overparen{BF} = \overparen{DE}\) (chứng minh trên)
Suy ra \(BF = DE\) (hai cung bằng nhau căng hai dây bằng nhau).
soanvan.me
