Đề bài
Tam giác \(ABC\) có độ dài các cạnh \(AB= m, AC= n\) và \(AD\) là đường phân giác. Chứng minh rẳng tỉ số diện tích tam giác \(ABD\) và diện tích tam giác \(ACD\) bằng \(\dfrac{m}{n}\).
Phương pháp giải - Xem chi tiết
Áp dụng: Công thức tính diện tích của tam giác, tính chất đường phân giác của tam giác.
Lời giải chi tiết
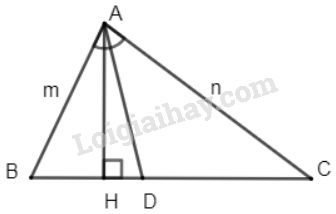
Gọi diện tích của tam giác \(ABD\) và \(ACD\) (h.18) lần lượt là \({S_{ABD}}; {S_{ACD}} \).
Gọi đường cao của tam giác là \(AH\).
\({S_{ABD}} = \dfrac{1}{2}BD.AH\)
\({S_{ACD}} = \dfrac{1}{2}DC.AH\)
\( \dfrac{S_{ABD}}{S_{ACD}} = \dfrac{\dfrac{1}{2}BD.AH}{\dfrac{1}{2}DC.AH} = \dfrac{BD}{DC}\)
Vì \(AD\) là đường phân giác của góc \(A\), nên ta có:
\( \dfrac{BD}{DC}= \dfrac{AB}{AC} = \dfrac{m}{n}\) (tính chất đường phân giác của tam giác)
Vậy \(\dfrac{S_{ABD}}{S_{ACD}} = \dfrac{m}{n}\) (đpcm).
soanvan.me
