Câu 7.
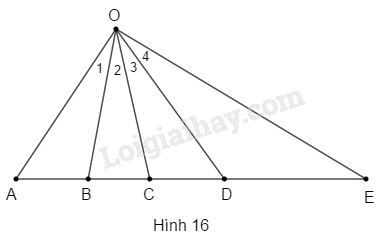
Cho biết \(\widehat {{O_1}} = \widehat {{O_2}} = \widehat {{O_3}} = \widehat {{O_4}}\). Hãy nhìn vào hình 16 rồi điền các tỉ số đúng vào những chỗ trống sau:
\(\begin{array}{l}
\dfrac{{AB}}{{BC}} = \dfrac{{....}}{{....}};\,\,\dfrac{{CD}}{{DE}} = \dfrac{{....}}{{....}}\\
\dfrac{{BC}}{{CD}} = \dfrac{{....}}{{....}};\,\,\dfrac{{AC}}{{CE}} = \dfrac{{....}}{{....}}
\end{array}\)
Phương pháp giải:
Phương pháp:
Sử dụng:
- Định lí: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn tỉ lệ với hai cạnh kề của hai đoạn ấy.
Lời giải chi tiết:
Lời giải:
Vì \(OB\) là tia phân giác của \(\widehat {AOC}\) nên ta có: \(\dfrac{{AB}}{{BC}} = \dfrac{{OA}}{{OC}}\).
Vì \(OD\) là tia phân giác của \(\widehat {COE}\) nên ta có: \(\dfrac{{CD}}{{DE}} = \dfrac{{OC}}{{OE}}\).
Vì \(OC\) là tia phân giác của \(\widehat {BOD}\) nên ta có: \(\dfrac{{BC}}{{CD}} = \dfrac{{OB}}{{OD}}\).
Vì \(OC\) là tia phân giác của \(\widehat {AOE}\) nên ta có: \(\dfrac{{AC}}{{CE}} = \dfrac{{OA}}{{OE}}\).
Câu 8.
Cho biết \(\widehat {{A_1}} = \widehat {{A_2}},\,AD = 3,5;\,BC = 4;\) \(CD = 2,5\) (h.17).
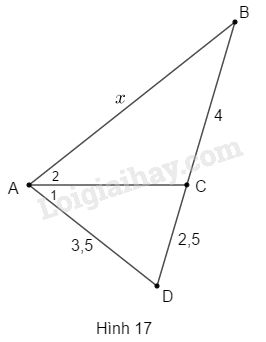
Độ dài \(x\) của \(AB\) là:
(A) \(5;\) (B) \(5,5;\) (C) \(5,6\).
Khoanh tròn vào chữ cái trước khẳng định đúng.
Phương pháp giải:
Phương pháp:
Sử dụng:
- Định lí: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn tỉ lệ với hai cạnh kề của hai đoạn ấy.
Lời giải chi tiết:
Lời giải:
Vì \(AC\) là tia phân giác của \(\widehat {DAB}\) nên ta có:
\(\begin{array}{l}
\dfrac{{CD}}{{AD}} = \dfrac{{CB}}{{AB}}\\
\Rightarrow \dfrac{{2,5}}{{3,5}} = \dfrac{4}{x}\\
\Rightarrow x = \dfrac{{3,5.4}}{{2,5}} = 5,6.
\end{array}\)
Chọn C.
soanvan.me
