Đề bài
a) Cho tam giác \(ABC\) với đường trung tuyến \(AM\) và đường phân giác \(AD\). Tính diện tích tam giác \(ADM\), biết \(AB= m, AC= n\;( n>m)\) và diện tích của tam giác \(ABC\) là \(S\).
b) Cho \(n = 7cm, m = 3cm\). Hỏi diện tích tam giác \(ADM\) chiếm bao nhiêu phần trăm diện tích tam giác \(ABC\).
Phương pháp giải - Xem chi tiết
Áp dụng: Tính chất đường phân giác trong tam giác. Trong một tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.
Lời giải chi tiết
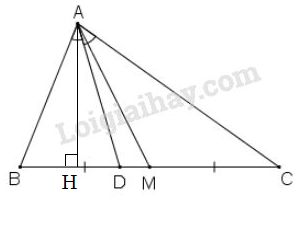
a) Từ tính chất của đường phân giác \(AD\) (h.22), ta có:
\(\dfrac{{B{\rm{D}}}}{{DC}} = \dfrac{{AB}}{{AC}}= \dfrac{m}{n}\)
Từ tính chất của tỉ lệ thức, ta có:
\(\dfrac{{BD}}{{DC + BD}} = \dfrac{m}{{n + m}}\)
hay \(\dfrac{{BD}}{{BC}} = \dfrac{m}{{n + m}} \Rightarrow BD = \dfrac{m}{{n + m}}BC\)
\(DM=BM-BD\)\(\,=\dfrac{1}{2}BC - \dfrac{m}{{n + m}}BC \)\(\,= \dfrac{{n + m - 2m}}{{2\left( {n + m} \right)}}BC\)
Rút gọn \(DM = \dfrac{{n - m}}{{2\left( {n + m} \right)}}BC.\)
Gọi \(AH\) là đường cao của \(\Delta ABC\).
\({S_{ADM}} = \dfrac{1}{2}DM.AH \)\(\,= \dfrac{1}{2}.\dfrac{{n - m}}{{2\left( {n + m} \right)}}.BC.AH\)
\({S_{ABC}} = \dfrac{1}{2}BC.AH\)
\(\dfrac{{{S_{ADM}}}}{{{S_{ABC}}}} = \dfrac{{n - m}}{{2\left( {n + m} \right)}}\)\(\, \Rightarrow {S_{ADM}} = \dfrac{{n - m}}{{2\left( {n + m} \right)}}{S}\)
b) \(\dfrac{{n - m}}{{2\left( {n + m} \right)}} = \dfrac{{\left( {n - m} \right).100}}{{2.\left( {n + m} \right).100}}\)\(\, = \dfrac{{\left( {7 - 3} \right).100}}{{2.\left( {7 + 3} \right).100}} \)\(\,= \dfrac{{20}}{{100}} = 20\% \)
Vậy \({S_{ADM}} = 20\% S.\)
soanvan.me
