Đề bài
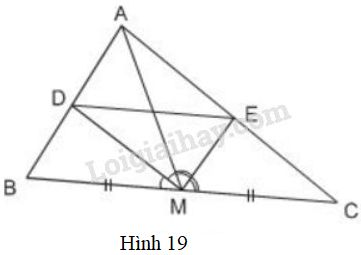
Cho tam giác \(ABC\) với đường trung tuyến \(AM\). Tia phân giác của góc \(AMB\) cắt cạnh \(AB\) ở \(D\), tia phân giác của góc \(AMC\) cắt cạnh \(AC\) ở \(E\). Chứng minh rằng \(DE // BC\) (h.19)
Phương pháp giải - Xem chi tiết
Áp dụng: Tính chất đường phân giác của tam giác, định lí TaLet đảo.
Lời giải chi tiết
Ta có \(MD\) là đường phân giác góc \(M\) của tam giác \(ABM\) (giả thiết)
\(\Rightarrow \dfrac{AD}{BD} = \dfrac{AM}{BM}\) (1) (tính chất đường phân giác của tam giác)
\(ME\) là đường phân giác góc \(M\) của tam giác \(ACM\) (giả thiết)
\(\Rightarrow \dfrac{AE}{CE}= \dfrac{AM}{MC}\) (2) (tính chất đường phân giác của tam giác)
Mà \(MB = MC\) (vì \(AM\) là đường trung tuyến nên \(M\) là trung điểm cạnh\(BC\))
\( \Rightarrow \dfrac{AM}{BM} = \dfrac{AM}{MC}\) (3)
Từ (1), (2), (3) \(\Rightarrow \dfrac{AD}{BD}= \dfrac{AE}{CE}\)
\( \Rightarrow DE // BC\) ( theo định lí Talet đảo).
soanvan.me
