Đề bài
Khi quay tam giác vuông để tạo ra một hình nón như hinh 87 thì góc \(CAO\) gọi là nửa góc ở đỉnh của hình nón. Biết nửa góc ở đỉnh của một hình nón là \(30^0\), độ dài đường sinh là \(a\). Tính số đo cung của hình quạt khi khai triển mặt xung quanh của hình nón.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+) Độ dài cung tròn có số đo \(n^0\) của đường tròn bán kính \(R\) là: \(l= \dfrac{\pi Rn}{180}.\)
+) Chu vi đáy hình nón với bán kính đáy r là: C= \(2\pi.r\)
Lời giải chi tiết
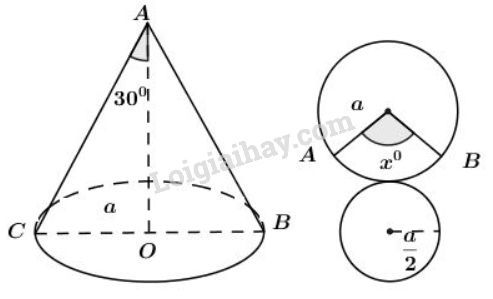
Vì \( \widehat {CAO}=30^0\) nên góc ở đỉnh của hình nón là \(\widehat {CAB}=2.30^0=60^0\)
Mà AB = AC
Nên \(∆ABC\) đều) (Tam giác cân có 1 góc bằng \(60^0\))
\(\Rightarrow BC = AB = AC=a\)
\(\Rightarrow\) Bán kính đáy của hình nón là:\( CO =\dfrac{BC}{2}=\dfrac{a}{2}\)
Chu vi đáy hình nón là \(C=2\pi.\dfrac{a}{2}=\pi .a\)
Đường sinh của hình nón là \(a.\) Khai triển mặt xung quanh hình nón ta được hình quạt AOB có bán kính \(R = a.\)
Độ dài cung AB có số đo \(x^0,\) bán kính \(a\) là \(l=\dfrac{\pi ax}{180}\)
Vì độ dài cung \(AB\) bằng chu vi đáy hình nón nên ta có:
\(\dfrac{\pi. ax}{180}=\pi .a\)
\(\Rightarrow\) \(x^0=180^0.\)
