Đề bài
Hình khai triển mặt xung quanh của một hình nón là một hình quạt, bán kính hình quạt đó là \(16cm,\) số đo cung là \(120^0.\) Tang của góc ở đỉnh hình nón là:
(A) \(\dfrac{\sqrt{2}}4\) (B) \(\dfrac{\sqrt{2}}2\) (C) \(\sqrt{2}\) (D) 2\(\sqrt{2}\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+) Ta có: \(h^2=l^2-r^2.\)
+) Gọi góc cần tính là \(\alpha.\) Khi đó: \(\tan \alpha=\dfrac{r}{h}.\)
Lời giải chi tiết
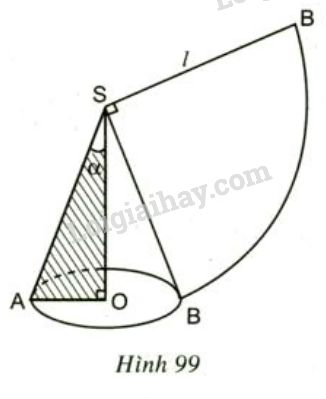
Đường sinh của hình nón là \(l = 16.\)
Độ dài cung \(AB\) của đường tròn chứa hình quạt là \(\dfrac {\pi .16.120}{180}=\dfrac{32. \pi}{3},\) và độ dài cung này bằng chu vi đáy hình nón \(C= 2πr\) suy ra \(2 \pi r=\dfrac{32. \pi}{3}\)\(\Rightarrow r= \dfrac{16}{3}.\)
Trong tam giác vuông \(AOS\) có: \(h= \sqrt{16^2-{\left( {\dfrac{{16}}{3}} \right)^2}}= 16\sqrt{\dfrac{8}{9}}= \dfrac{32\sqrt{2}}{3}\)
Vậy ta có: \(\tan \alpha= \dfrac{r}{h} = \dfrac{\sqrt{2}}{4}.\)
Chọn A.
soanvan.me
