Đề bài
Cho nửa đường tròn tâm \(O\), đường kính \(AB\) và dây \(EF\) không cắt đường kính. Gọi \(I\) và \(K\) lần lượt là chân các đường vuông góc kẻ từ \(A\) và \(B\) đến \(EF\). Chứng minh rằng \(IE = KF.\)
Phương pháp giải - Xem chi tiết
+ Áp dụng định lí : Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.
+ Áp dụng tính chất đường trung bình của hình thang: Đường thẳng đi qua trung điểm cạnh bên thứ nhất và song song với hai đáy thì đi qua trung điểm cạnh bên thứ hai.
Lời giải chi tiết
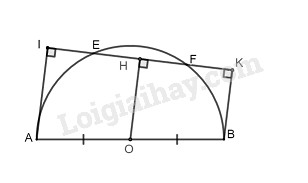
Ta có: \(AI ⊥ EF\) (gt)
\(BK ⊥ EF\) (gt)
Suy ra: \(AI // BK\)
Suy ra tứ giác \(ABKI\) là hình thang
Kẻ \(OH ⊥ EF\)
Suy ra: \(OH // AI // BK\) (cùng vuông với IK)
Ta có: \(OA = OB (= R)\)
Như vậy hình thang \(ABKI\) có OH đi qua trung điểm cạnh bên AB và song song với hai đáy AI, BK nên OH đi qua trung điểm cạnh bên IK.
Suy ra: \(HI = HK\)
Hay:
\( HE + EI = HF+FK \) (1)
Xét đường tròn (O) có OH là một phần đường kính, EF là dây của đường tròn.
Vì \(OH\bot EF\) nên \(HE = HF\) (2) (quan hệ giữa đường kính và dây cung)
Từ (1) và (2) suy ra:\( IE = KF.\)
soanvan.me
