Đề bài
Cho đường tròn \((O; R)\) và điểm \(M\) nằm bên trong đường tròn.
a) Hãy nêu cách dựng dây \(AB\) nhận \(M\) làm trung điểm.
b) Tính độ dài \(AB\) ở câu a) biết rằng \(R = 5cm\); \(OM = 1,4cm\).
Phương pháp giải - Xem chi tiết
Dựng hình:
+ Dựng đoạn \(OM\), từ \(M\) dựng đường vuông góc với \(OM\)
Chứng minh:
+ Sử dụng: Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy để chứng minh.
Lời giải chi tiết
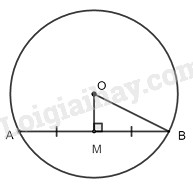
a) * Cách dựng
− Dựng đoạn \(OM.\)
− Qua \(M\) dựng đường thẳng vuông góc với \(OM\) cắt \((O)\) tại \(A\) và \(B.\)
Nối \(A\) và \(B\) ta được dây cần dựng.
* Chứng minh
Xét (O) có \(OM ⊥ AB\) mà \(OM\) là 1 phần đường kính và AB là dây của đường tròn \(⟹MA = MB=\dfrac{AB}2.\)
b) Áp dụng định lí Pi-ta-go vào tam giác vuông OMB, ta có:
\(O{B^2} = O{M^2} + M{B^2}\)
Suy ra:
\(M{B^2} = O{B^2} - O{M^2}\)\( = {5^2} - 1,{4^2} = 25 - 1,96 = 23,04\)
\(MB = 4,8\)(cm)
Vậy \(AB = 2.MB = 2.4,8 = 9,6 (cm).\)
soanvan.me
