Đề bài
Cho đường tròn \((O; R)\), dây \(AB\) khác đường kính. Vẽ về hai phía của \(AB\) các dây \(AC, AD.\) Gọi \(H\) và \(K \) theo thứ tự là chân các đường vuông góc kẻ từ \(B\) và \(AC\) và \(AD.\) Chứng minh rằng:
a) Bốn điểm \(A, H, B, K\) thuộc cùng một đường tròn;
b) \(HK < 2R.\)
Phương pháp giải - Xem chi tiết
Ta sử dụng các kiến thức sau:
+ Để chứng minh các điểm thuộc cùng một đường tròn ta chứng minh các điểm này cách đều một điểm.
+ Trong các dây của một đường tròn, dây lớn nhất là đường kính.
Lời giải chi tiết
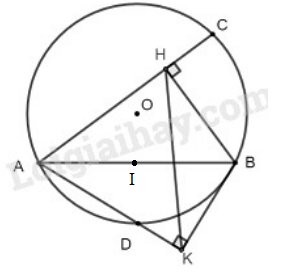
a) Ta có: \(\widehat {AHB} = \widehat {AKB} = {90^o}\)
Do đó tam giác AKB vuông tại K, tam giác AHB vuông tại H nên \(H\) và \(K\) cùng thuộc một đường tròn đường kính \(AB.\)
Vậy bốn điểm \(A, H, B, K\) cùng thuộc một đường tròn đường kính \(AB.\)
b) Gọi \(I\) là trung điểm của \(AB.\)
\(HK\) là dây cung không đi qua tâm \(I\) của \(\left( {I,\dfrac{{AB}}{2}} \right)\)
Do đó: \(HK < AB\) (1)
Mặt khác: \(AB\) là dây cung không đi qua tâm \(O\) của \((O,R)\) nên \(AB<2R\) (2)
Từ (1) và (2) ta có: \(HK < AB < 2R\).
soanvan.me
