Đề bài
Cho tam giác \(ABC\). Hãy vẽ một tam giác đồng dạng với tam giác \(ABC\) theo tỉ số \(\dfrac{1}{2}\).
Phương pháp giải - Xem chi tiết
Áp dụng định lí: Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác đồng dạng với tam giác đã cho.
Lời giải chi tiết
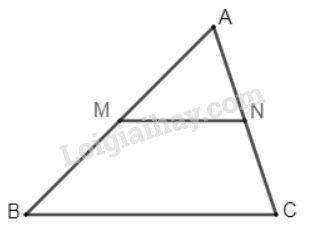
1. Cách dựng:
Trên cạnh \(AB\), dựng điểm \(E\) sao cho \(AE = \dfrac{1}{2}AB\).
Trên cạnh \(AC\), dựng điểm \(F\) sao cho \(AF = \dfrac{1}{2}AC\).
Tam giác \(AEF\) là tam giác phải dựng (h.24).
2. Chứng minh:
Từ cách dựng ta có: \(\dfrac{{AE}}{{AB}} = \dfrac{1}{2};\dfrac{{AF}}{{AC}} = \dfrac{1}{2}\) \( \Rightarrow \dfrac{{AE}}{{AB}} = \dfrac{{AF}}{{AC}}.\)
Áp dụng định lý Ta – let đảo, suy ra \(EF//BC\).
Áp dụng định lý bài 4, ta suy ra \(\Delta AEF \backsim \Delta ABC\) theo tỉ số \(\dfrac{{AE}}{{AB}} = \dfrac{1}{2}\).
soanvan.me
