Bài 20 trang 68 Vở bài tập toán 9 tập 1

Đề bài

a) Vẽ đồ thị của các hàm số sau trên cùng một mặt phẳng tọa độ:

\(y = \dfrac{2}{3}x + 2;\,\,y =  - \dfrac{3}{2}x + 2\)

b) Một đường thẳng song song với trục hoành Ox, cắt trục tung Oy tại điểm có tung độ bằng 1, cắt các đường thẳng \(y = \dfrac{2}{3}x + 2\) và \(y =  - \dfrac{3}{2}x + 2\) theo thứ tự tại hai điểm M và N. Tìm tọa độ của hai điểm M và N.

Lời giải chi tiết

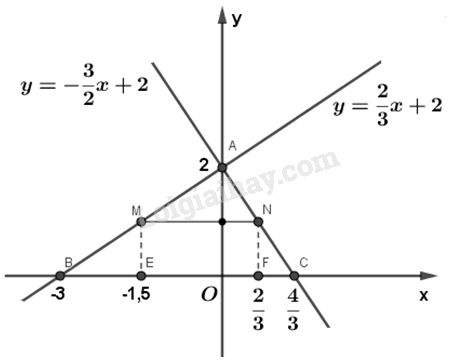
a) Vẽ đồ thị hàm số \(y = \dfrac{2}{3}x + 2\):

+) Cho \(x = 0\) thì \(y = 2\), được điểm \(A\left( {0;2} \right)\)

+) Cho \(y = 0\) thì \(x =  - 3\) , được điểm \(B\left( { - 3;0} \right)\)

Vẽ đường thẳng đi qua hai điểm A và B, được đồ thị của hàm số \(y = \dfrac{2}{3}x + 2\)

Vẽ đồ thị của hàm số \(y =  - \dfrac{3}{2}x + 2\)

+) Cho \(x = 0\) thì \(y = 2\) , được điểm \(A\left( {0;2} \right)\)

+) Cho \(y = 0\) thì \(x = \dfrac{4}{3}\) , được điểm \(C\left( {\dfrac{4}{3};0} \right)\)

Vẽ đường thẳng đi qua hai điểm A và C, được đồ thị của hàm số \(y =  - \dfrac{3}{2}x + 2\).

b) Tọa độ của điểm M :

Điểm M có tung độ \(y = 1\)

Thay giá trị \(y = 1\)  vào phương trình \(y = \dfrac{2}{3}x + 2\) để tìm x, ta có :

\(1 = \dfrac{2}{3}x + 2 \Rightarrow \dfrac{2}{3}x =  - 1 \Rightarrow x = \left( { - 1} \right):\dfrac{2}{3} =  - \dfrac{3}{2}\)

Vậy ta có \(M\left( { - \dfrac{3}{2};1} \right)\)

Tọa độ của điểm N :

Điểm N có tung độ \(y = 1\)

Thay giá trị \(y = 1\) vào phương trình \(y =  - \dfrac{3}{2}x + 2\) để tìm x, ta có :

\(1 =  - \dfrac{3}{2}x + 2 \Rightarrow \dfrac{3}{2}x = 1 \Rightarrow x = \dfrac{2}{3}\)

Vậy ta có : \(N\left( {\dfrac{2}{3};1} \right)\)

soanvan.me