Cho hình chóp \(S.ABCD\) có đáy là tứ giác \(ABCD\) có hai cạnh đối diện không song song. Lấy điểm \(M\) thuộc miền trong của tam giác \(SCD\). Tìm giao tuyến của hai mặt phẳng:
LG a
\((SBM)\) và \((SCD)\)
Phương pháp giải:
Muốn tìm giao tuyến của hai mặt phẳng ta tìm hai điểm chung của chúng.
Lời giải chi tiết:
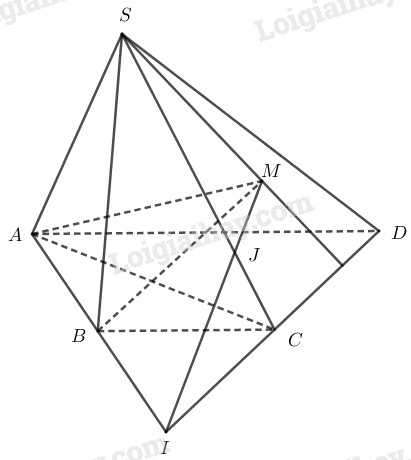
Ta có \(S\), \(M\) là hai điểm chung mặt phẳng \((SBM)\) và \((SCD)\).
Vậy \((SBM) \cap (SCD) = SM\).
LG b
\((ABM)\) và \((SCD)\)
Phương pháp giải:
Muốn tìm giao tuyến của hai mặt phẳng ta tìm hai điểm chung của chúng.
- Điểm chung thứ nhất thường nhìn thấy luôn.
- Điểm chung thứ 2: tìm hai đường thẳng lần lượt thuộc hai mặt phẳng, đồng thời chúng lại thuộc mặt phẳng thứ ba và chúng không song song. Giao điểm của hai đường thẳng đó là điểm chung thứ hai. Trong bài này hai đường thẳng đó thuộc mặt phẳng đáy.
Lời giải chi tiết:
Ta có \(M\) là điểm chung thứ nhất
Gọi \(I = AB \cap CD\)
Khi đó \(I \in AB \Rightarrow I \in (ABM)\), \(I \in CD \Rightarrow I \in (SCD)\).
Do đó \(I\) là điểm chung thứ hai.
Vậy \((ABM) \cap (SCD) = IM\).
LG c
\((ABM)\) và \((SAC)\)
Phương pháp giải:
Muốn tìm giao tuyến của hai mặt phẳng ta tìm hai điểm chung của chúng.
- Điểm chung thứ nhất thường nhìn thấy luôn.
- Điểm chung thứ 2: tìm hai đường thẳng lần lượt thuộc hai mặt phẳng, đồng thời chúng lại thuộc mặt phẳng thứ ba và chúng không song song. Giao điểm của hai đường thẳng đó là điểm chung thứ hai. Trong bài này mặt phẳng \((ABM)=(ABIM)\), từ đó ta tìm được hai đường thẳng cần lấy giao.
Lời giải chi tiết:
Ta có \(A=(ABM) \cap (SAC)\)
Gọi \(J = IM \cap SC\).
Khi đó \(J \in IM \Rightarrow J \in (ABM)\) và \(J \in SC \Rightarrow J \in (SAC)\).
Do đó \(J \in (ABM) \cap (SAC)\)
Vậy \((ABM) \cap (SAC) = AJ\)
soanvan.me
